[удалено]
-- 22.12.2025, 23:01 --Ну вот если положить центр графа за

, а центр сферы

, тогда остальные шесть точек должны находится на пересечении сферы и плоскости:
1)

2)
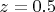
Отсюда:
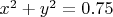
Радиус окружности есть ничто иное как
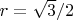
. Однако тогда заветное расстояние не равно 1. Спасибо за контрпример. Но что если положить максимальное расстояние между вершинами не

, а

? Найдется ли меньший контрпример?