В учебнике М. И. Дьяченко, П. Л. Ульянов Мера и интеграл. - М., 1998. так описывается построение меры Лебега-Стильтеса на отрезке.
Пусть

-- действительная функция ограниченной вариации на отрезке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
. Представим её в виде разности двух возрастающих функций
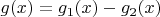
, где
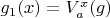
-- полная вариация функции

на отрезке
![$[a,x]$ $[a,x]$](https://dxdy-04.korotkov.co.uk/f/7/8/8/78803621c5e4e61a79d2880c449812f382.png)
. Продолжим функции

и

на всю прямую, полагая

при

и
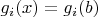
при

. Переопределим значения функций

в точках разрыва, сделав их непрерывными слева. На полукольце

определим две меры
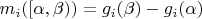
,
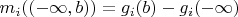
, где
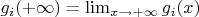
,
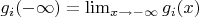
. Эти меры будут

-аддитивны на

(благодаря непрерывности слева). Продолжим каждую из них по Лебегу до мер
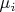
, заданных на

-алгебре

подмножеств числовой прямой. Тогда на

-алгебре
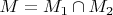
определен заряд
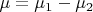
. Ограничение этого заряда на

-алгебру
![$M\cap [a,b]=\{A\in M\mid A\subset [a,b]\}$ $M\cap [a,b]=\{A\in M\mid A\subset [a,b]\}$](https://dxdy-02.korotkov.co.uk/f/d/2/f/d2f38dd607f9572f2b8e06bd0230d7b182.png)
и будет искомой мерой Лебега-Стилтьеса (точнее зарядом).
У меня такой вопрос: как доказать, что полная вариация

заряда

совпадает с мерой

, порождаемым функцией
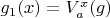
? Я могу только доказать, что
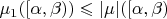
для любого полуинтервала
![$[\alpha,\beta)\subset [a,b]$ $[\alpha,\beta)\subset [a,b]$](https://dxdy-02.korotkov.co.uk/f/1/a/9/1a9eb924b2255f2135beeecb46ca76a482.png)
. Это следует из формулы
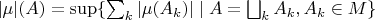
и того, что при подходящем разбиении
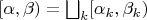
будет
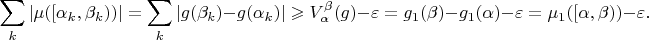
Как доказать противоположное неравенство

?
И как от полуинтервалов перейти к произвольным измеримым множествам  ?
?Как от полуинтервалов перейти к произвольным множествам, понял: надо ипользовать свойство однозначности продолжения меры по Лебегу (см. Колмогоров, Фомин). Любое множество

(даже
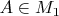
) обладает следующим свойством: для любой

-аддитивной меры

, определённой на

-алгебре, содержащей множество

, и совпадающей с

на полукольце

полуинтервалов, выполнено
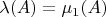
. Мера

--

-аддитивная мера, заданная на

алгебре

, содержащей множество

. Поэтому достаточно доказать, что она совпадает с

на полуинтервалах.