Оценка ошибки решения СЛАУ

[B@R5uk]

Пусть известна матрица A и столбец свободных членов b системы линейных уравнений:

$$Ax=b$$

Система недоопределена, и ранг матрицы A равен числу сток (полный ранг). Решение находится через псевдообратную матрицу:

$$x=A^+b$$

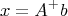
Известна так же оценка ошибки ε, на которую отличается известная матрица A от "оригинальной" (но неизвестной):

$$A=A_0+E$$

$$|E_{ij}|\le\varepsilon$$

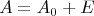
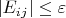
Задача состоит в том, чтобы определить как сильно решение x возмущённой системы с матрицей A отличается от оригинального решения:

$$x_0=A_0^+b$$

$$\lVert x-x_0\rVert=?$$

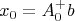
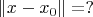
Интуиция подсказывает, что должно получиться что-нибудь в духе

$$\lVert x-x_0\rVert\sim\frac{\lVert E\rVert\cdot\lVert x\rVert}{\sigma_{min}(A)}$$

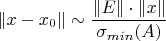
Где σ — это последнее (наименьшее) сингулярное число матрицы A. По аналогии с формулой для полной системы с квадратной матрицей A:

$$\lVert x-x_0\rVert_2\le\lVert A^{-1}\rVert_2\cdot\lVert E\rVert_2\cdot\lVert x\rVert_2$$

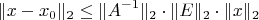
Но как это доказать? Подскажите, пожалуйста как быть или где почитать?

[B@R5uk]

Оке, эти ваши искусственные интеллекты разрослись не по-детски! Три запроса в Гугловый ИИ, и он все секреты мироздания выдал с потрохами. Я так и знал, что эта задача стандартная и востребованная.

Статьи (классика 70-х):

• Perturbation theory for pseudo-inverses - P.-A. Wedin (1973)
• On the Perturbation of Pseudo-Inverses, Projections and Linear Least Squares Problems - G.W. Stewart (1977)

Учебники (классика 90-х):

• Gene H. Golub, Charles F. Van Loan - Matrix computations (1996, 3rd ed)
• Ake Bjorck - Numerical methods for least squares problems (1996)

Последние статьи (современное наведение лоска):

• The optimal perturbation bounds of the Moore-Penrose inverse under the Frobenius norm - Lingsheng Meng, Bing Zheng (2010)
• Multiplicative perturbation theory of the Moore-Penrose inverse and the least squares problem - N. Castro-Gonzalez, F.M. Dopico, J.M. Molera (2016)

Статьи качнул, буду осваивать всё. Учебники уже были давно скачаны, я даже Голуба-ВанЛоана перерыр в поисках оценок, но не нашёл. Оказывается они там в разделы про МНК запрятаны.

[B@R5uk]

Что-то как-то формулы близки, прям таки что надо, но чуть-чуть не те. Вот, например вот эта:

$$x=A^+b$$

$$x+\delta x=(A+\delta A)^+b$$

$$\lVert\delta x\rVert_2\le\frac{\lVert\delta A\rVert_2\lVert x\rVert_2}{\sigma_n(A)}+\frac{\lVert\delta A\rVert_2\lVert r\rVert_2}{\sigma^2_n(A)}$$

$$r=b-Ax$$

которая (вроде бы как) работает, когда ранги исходной матрицы A и возмущённой равны между собой и числу столбцов n (погрешность, связанную с ошибкой в столбце b я выкинул, потому что он у меня задан точно). Но в этих формулах матрица A — это исходная матрица. Через неё всё считается, но я её не знаю, знаю только возмущённую. Можно что-то с этим сделать?

В других формулах всё то же самое, только в знаменателе добавляется множитель

$$1-\eta=1-\lVert A^+\rVert_2\lVert\delta A\rVert_2=1-\frac{\lVert\delta A\rVert_2}{\sigma_n(A)}$$

Он явно ухудшает точность, особенно на гране смены ранга. Не совсем понятно, где правильнее.

Подскажите, пожалуйста, в этом вопросе, кому не сложно.