Задача из учебника по вариационному исчислению

[DTF]

Учебника Александрова и Егорова "Вариационное исчисление".

Задача № 18:
Докажите, что всякое уравнение $y'' =f(x, y, y')$ является уравнением Эйлера для некоторого функционала $I[y] = \int\limits_{x_0}^{x_1} F(x, y, y')dx$.
Как определяется функция F по функции f?

В ответах/указаниях написано вот это:
$u = F_{y'y'}$ удовлетворяет уравнению $u_x + y'u_y + fu_{y'} + f_{y'}u = 0$.

У меня типичная проблема, когда пытаешься в чем-то разобраться самостоятельно - не понятно вообще ничего :)
Поясните плс, как нужно решать эту задачу и при чем тут это уравнениею

Я даже не уверен, что правильно понял обозначения.
$F_{y'y'}$ - это вторая частная производная по $y'$ ?
А $u_x, u_{y'}$ - частная производная по x и $y'$ соответственно?

[пианист]

DTF в сообщении #1712398 писал(а):

Я даже не уверен, что правильно понял обозначения.

Да, все правильно.

Надо в уравнении ЭЛ вместо $y''$ подставить то, чему оно должно быть предположительно равно (т.е. $f$), собс-но, мы так и получим уравнение на $F$.
Только Александров и Егоров, чтобы ученикам было не скучно, видимо ;), в ответе дополнительно еще продифференцировали его по $y'$.

[DTF]

пианист в сообщении #1712403 писал(а):

Надо в уравнении ЭЛ вместо $y''$ подставить то, чему оно должно быть предположительно равно (т.е. $f$), собс-но, мы так и получим уравнение на $F$

Что такое "Уравнение ЭЛ" ?

[Null]

Эйлера-Лагранжа

[DTF]

Я не понимаю как это сделать:
Уравнение Эйлера выглядит так:

$F_y - \frac{d}{dx}F_{y'} = 0$, если переобозначить, то можно написать так:

$F_{y'} - \frac{d}{dx}F_{y''} = 0$.

В любом случае, тут фигурируют производные искомой функции F, куда мы подставляем $y'' = f$ ?
Если же мы пытаемся представить себе, что само уравнение $y'' = f$ - это уравнение Эйлера,
и пытаемся приравнять стороны уравнения, например вот так:
$\frac{d}{dx}F_{y''} = y''$

$F_{y'}= f$
То всё равно непонятно, как найти F.
Мб тут используется какая-то всем известная теорема из курса дифуров, которую я уже не помню?

[пианист]

DTF в сообщении #1712441 писал(а):

если переобозначить

Такое переобозначение представляется бессмысленным действием. Дальнейшее вообще непонятно, что такое.

DTF в сообщении #1712441 писал(а):

куда мы подставляем $y'' = f$ ?

Если Вас интересует, откуда в уравнении ЭЛ $y''$, то ответ: из полной производной $F_{y'}$.
$\frac{d} {dx} F_{y'} = F_{xy'} +y'F_{yy'} + y''F_{y'y'}$.

[DTF]

Спасибо за ответ, но я всё равно не понимаю

Пусть мы записали уравнение Эйлера в виде
$F_y = F_{xy'} + y'F_{yy'} + y''F_{y'y'}$
Сделали замену $u = F_{y'y'}$, а также подставили $y'' = f$

Получаем $F_y = F_{xy'} + y'F_{yy'} + fu$

Что это нам даёт? Можно попробовать продифференцировать обе части по y' и посмотреть что получится,
но там как-то много вычислений, я не уверен что это правильный путь.
Или всё же правильный, и их надо проделать?

Далее, я Вас понял, что в формуле $u_x + y'u_y + fu_{y'} + f_{y'}u = 0$ в левой части написано $u_{y'}$, т.е. мы имеем $F_{y'y'y'} = u_{y'} = 0$

Но
1. Почему эта производная равна нулю? Или почему мы приравниваем её к нулю?
2. И что нам даёт её равенство нулю?

[lel0lel]

DTF в сообщении #1712570 писал(а):

Или всё же правильный, и их надо проделать?

Да, нужно проделать (производная по $y'$ частная, будет не так много вычислений) и снова перейти к $u$.

[пианист]

DTF в сообщении #1712570 писал(а):

Далее, я Вас понял, что в формуле $u_x + y'u_y + fu_{y'} + f_{y'}u = 0$ в левой части написано $u_{y'}$, т.е. мы имеем $F_{y'y'y'} = u_{y'} = 0$

Не понял. Что значит "написано" - что в левой части присутствует $u_{y'}$? присутствует, и что. Почему оно ноль?
Так-то я согласен с уважаемым lel0lel: продифференцировать там совсем не сложно; собс-но, даже в уме можно, сразу видно же, что сокращается.

(Оффтоп)

Позволите встречный вопрос? Для чего Вам вообще понадобилась эта задача?
Можно же прекрасно жить, не имея представления о том, как по уравнению восстановить лагранжиан, да и вообще об уравнениях и лагранжианах. ;)

[DTF]

Ага, я не сообразил, что можно частную производную взять вместо полной.

После взятия производной я получил выражение с u, которое было в ответе.

Но я по-прежнему не понимаю, что оно нам дает?
Почему из того, что в результате дифференцирования получилось это выражение, следует,
что $y'' = f$ - это уравнение Эйлера для какого-то функционала.

Я понимаю, что на этом форуме не принято давать решение полностью, но я похоже не понял материал учебника.
Объясните, пожалуйста, в целом, как решается эта задача.

[пианист]

DTF в сообщении #1712659 писал(а):

Почему из того, что в результате дифференцирования получилось это выражение, следует,
что $y'' = f$ - это уравнение Эйлера для какого-то функционала.

Уравнение ЭЛ, в котором вместо $y''$ подставили $f$, это в точности условие того, что оно, уравнение ЭЛ, приводится к виду $y''=f$. Или в чем вопрос?

[DTF]

Наконец-то добрался до форума

пианист в сообщении #1712692 писал(а):

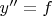
Уравнение ЭЛ, в котором вместо $y''$ подставили $f$, это в точности условие того, что оно, уравнение ЭЛ, приводится к виду $y''=f$. Или в чем вопрос?

Разве?
Мне казалось, что "привести уравнение к виду" - то значит

• Взять исходное уравнение $y'' = f$
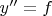
• Сделать какие-то преобразования
• Сделать замену F = <что-то>
• Снова сделать какие-то преобразования
• В результате получить $F_y - \frac{d}{dx}F_{}y' = 0$

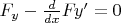
Ну или наоборот, имея уравнение Эйлера, взять F какого-то специального вида,
и из него получить $y'' = f$.

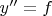
Т.е., в моем понимании, "привести к виду" - значит взять исходное уравнение, преобразовать его, получить требуемое уравнение.

А у меня пока что получается, что я в уравнение Эйлера подставил значение и получил некую формулу (которая была в ответе).

Ну так в любое уравнение можно что-то подставить и что-то в результате получить.
Что это доказывает?

-- 28.12.2025, 07:35 --

(Оффтоп)

пианист в сообщении #1712583 писал(а):

Позволите встречный вопрос? Для чего Вам вообще понадобилась эта задача?
Можно же прекрасно жить, не имея представления о том, как по уравнению восстановить лагранжиан, да и вообще об уравнениях и лагранжианах. ;)

(Оффтоп)

Прошу пардона, я не увидел вовремя Ваше сообщение.
Задача понадобилась потому, что она идет после параграфа в учебнике.
Такие задачи обычно решаются очень просто, но для их решения требуется понимание материала параграфа.
Из того, что я не могу решить эту задачу следует, что материал я не понял :)

[пианист]

Ну пожалуйста, давайте по Вашему. Пусть у нас есть диффур $y''=f$ (*).
Предположим, мы представили $f$ в виде
$f=\frac {F_y-F_{xy'} - y'F_{yy'}} {F_{y'y'}} $ (**).
Заменяя в (*) $f$ из (**), умножая на $F_{y' y'} $ и перенося все в одну сторону, получаем уравнение ЭЛ.
Стало быть, вопрос в возможности представить $f$ в виде (**). Но если проделать с (**) те же манипуляции (умножить, перенести), мы получим уравнение ЭЛ, в котором вместо $y''$ подставили $f$.

DTF в сообщении #1713435 писал(а):

Задача понадобилась потому, что она идет после параграфа в учебнике.

Это, я бы сказал, очень факультативное. Не решив хоть пару примеров на конкретное вычисление экстремалей, ее не стоит трогать. Да и вообще, честно говоря, не стоит ;)