Эпиморфный образ

[OlgaD]

Я пытаюсь понять разницу между двумя понятиями - образом морфизма и его эпиморфным образом. Кажется, интуиция с категорией множеств меня подводит. Пусть у нас есть морфизм $f:A\to B$ в некоторой категории и пусть $(I,m)$ - его (категорный) образ. Всегда ли мы тогда имеем разложение: $f=m\circ e,$ где $e$ - эпиморфизм? Если это так, то тогда зачем определять эпиморфный образ как образ, в котором $e$ - эпиморфизм? Это же и так выполняется. Вот если бы потребовали, чтобы $m:I\to B$ было также эпиморфизмом, тогда в сбалансированных категориях это означало бы, что $m$ - изоморфизм, т.е. $f$ - эпиморфизм.

[dgwuqtj]

OlgaD в сообщении #1712070 писал(а):

Всегда ли мы тогда имеем разложение: $f=m\circ e,$ где $e$ - эпиморфизм?

Не всегда. Возьмём свободную категорию с объектами $A, B, C, D$, порождённую морфизмами $f_1, f_2 \colon A \to B$, $g \colon B \to C$ и $h_1, h_2 \colon B \to C$. В ней всего 17 морфизмов. Тогда $g$ не мономорфизм и не эпиморфизм. Его категорный образ — это $\mathrm{id}_C$.

[OlgaD]

С понятием свободной категории я пока не знакома. А в каких категориях это разложение имеет место?

[dgwuqtj]

OlgaD в сообщении #1712081 писал(а):

С понятием свободной категории я пока не знакома.

А с понятием свободной группы и свободного модуля знакомы? Речь идёт просто про категорию с морфизмами $\mathrm{id}_A, \mathrm{id}_B, \mathrm{id}_C, \mathrm{id}_D, f_1, f_2, g, h_1, h_1, h_i \circ g, g \circ f_j, h_i \circ g \circ f_j$. Можно эту категорию реализовать как-то конкретно, скажем, $A = \{ 0 \}$, $B = \{ 1, 2 \}$, $C = \{ 3, 4 \}$, $D = \{ 5, 6, 7, 8 \}$, $f_i(0) = i$, $g(t) = t$, $h_1(t) = t + 2$, $h_2(t) = t + 4$.

OlgaD в сообщении #1712081 писал(а):

А в каких категориях это разложение имеет место?

Есть такой замечательный класс регулярных категорий. Если неформально, это те категории, где есть конечные пределы и хорошо ведущие себя образы морфизмов. Только в регулярных категориях тоже бывают неинтуитивные вещи, скажем, морфизм $\mathbb Z \to \mathbb Q$ в категории колец с единицей является необратимым мономорфизмом и эпиморфизмом (т.е. это эпиморфизм, у которого образ строго меньше области значений).

[OlgaD]

Спасибо. Тогда уж сопутствующий вопрос. Если потребовать эпиморфности не от морфизма $e,$ а от $m,$ получим ли мы в этом случае изоморфизм $\mathrm{im}(f)\cong Y?$

[dgwuqtj]

То есть верно ли, что у эпиморфизма $f \colon X \to Y$ образом будет $Y$? Нет, выше же написан пример $\mathbb Z \to \mathbb Q$ в категории колец без единицы.

[OlgaD]

Меня все время сносит в категорию множеств. Однако можно ли сформулировать условия, при которых образ морфзма $f$ будет как раз $Y?$

[dgwuqtj]

Ну, например, если у вас предтопос, то все эпиморфизмы будут регулярными и тогда их образы — это в точности области значений. Просто регулярные категории встречаются часто: это и категории любых алгебраических структур (групп, колец, модулей и т.д.), и абелевы категории, и категория множеств, и категории пучков. А предтопосы — это категория множеств, категории пучков, ну и всякая экзотика.

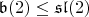
Хотя в категории групп и во всех абелевых категориях все эпиморфизмы тоже регулярны, для групп это вообще не очевидно (что эпиморфизмы — это сюръективные гомоморфизмы). А вот уже в категории конечномерных алгебр Ли над $\mathbb C$ это не так, хотя, казалось бы, это что-то похожее на группы. Пример — подалгебра верхнетреугольных матриц с нулевым следом $\mathfrak b(2) \leq \mathfrak{sl}(2)$, её вложение является эпиморфизмом.

[OlgaD]

Я начиталась Голдблатта Топосы, категорный анализ логики. У него почти каждое описание конструкции в теории категорий начинается с интуитивно понятного примера в категории множеств. И он как-то понятие эпиморфного образа обошол стороной.

[OlgaD]

Если я правильно понимаю, epi-mono факторизация морфизма чере его образ также возможна не во всех категориях, но возможна в регулярных категориях?

[dgwuqtj]

OlgaD в сообщении #1712131 писал(а):

И он как-то понятие эпиморфного образа обошол стороной.

Видимо, это понятие ему не нужно. Вообще в любом разделе математики есть куча редко используемой терминологии, ну так всю терминологию и не надо изучать.

OlgaD в сообщении #1712141 писал(а):

Если я правильно понимаю, epi-mono факторизация морфизма чере его образ также возможна не во всех категориях, но возможна в регулярных категориях?

Что-то в этом духе. В регулярных категориях говорят про разложение в композицию мономорфизма и регулярного эпиморфизма, оно там существует, единственно и функториально по раскладываемому морфизму. В той же категории колец с единицей есть куча способов разложить $\mathbb Z \to \mathbb Q$ в композицию мономорфизма и эпиморфизма, хотя бы как $\mathbb Z \to \mathbb Z[\frac 1 n] \to \mathbb Q$.

[OlgaD]

Изучать всю терминалогию и все разделы математики я не собираюсь... Но, думаю, мне крайне полезно было узнать, что не все образы эпиморфны. Это как взгляд с высоты на привычные понятия.