Точки в круге

[staric]

Можно ли в круге единичного радиуса отметить по 7 синих и красных точек так, чтобы расстояние между точками одного цвета составило не менее $\frac{\pi}{4}$, а между точками разных цветов не менее $\frac{1}{2}$ ?

[waxtep]

Кажется, можно; я правда под конец запутался в углах и вычислениях, поэтому только как идея, без претензии на решение. В вычислениях часто возникает величина $\sqrt{2-\sqrt3}$, что как раз чуть больше $1/2$, и это вселяет надежду.

Разместим шесть красных точек в вершинах вписанного правильного шестиугольника; пусть одна из них строго над центром окружности, а другая под. Четыре синих точки разместим на окружности как можно ниже, по две симметрично относительно вертикального диаметра, а еще две, наоборот, повыше (не факт, что максимально высоко; на этом месте я оставил вычисления). Наконец, разместим седьмую красную точку на вертикальном диаметре как можно ниже; и седьмую синюю как можно ниже над ней.

[svv]

У меня идея похожая, но симметричная конфигурация не получилась.

Вложение:

a.png

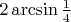
Точки расставляются в порядке нумерации. Точки 0 и 1 понятно где. Остальные точки на окружности прижимаются, насколько возможно, к ранее поставленному правому соседу на окружности (то есть между ними угол $2\arcsin\frac 1 4$, лишь дуги 0-10 и 0-11 будут больше).
Точка 12 находится на $Ox$ как можно ближе к точкам 10 и 11.
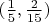
Тогда для красной точки 13 остаются две крохотных клиновидных области выше и ниже $Ox$, которые, увы, не смыкаются. Координаты можно выбрать, например, $(\frac{1}{5}, \frac{2}{15})$.

[waxtep]

svv в сообщении #1712032 писал(а):

Тогда для красной точки 13 остаются две крохотных клиновидных области выше и ниже $Ox$, которые, увы, не смыкаются

Ух ты! Дааа. Интересно, существует ли осесимметричное решение

[staric]

svv Отличное решение! Посчитаете, какое максимальное расстояние между одноцветными обеспечивает такой подход (при тех же 0.5 между разноцветными)?

waxtep писал(а):

Интересно, существует ли осесимметричное решение

Существует. Уверен, сможете найти.