Если устроят неполные пространства - то многочлены на
![$[-1, 1]$ $[-1, 1]$](https://dxdy-01.korotkov.co.uk/f/4/3/c/43ca5ad9e1f094a31392f860ef481e5c82.png)
с

-нормой.
Хммм, а разве если последовательность многочленов равномерно сходится к какой-то функции (в таком случае она будет аналитической, то есть в каком-то смысле бесконечным многочленом), то коэффициенты не будут соответствующие тоже сходиться?
Да и если мы рассматриваем именно пространство многочленов (неполное), то пределом там может быть только многочлен (небесконечный в смысле), уж там-то, кажется, заведомо коэффициенты должны сходиться к соответствующему коэффициенту... мне кажется, это можно даже в

-норме доказать, а тем более в супремумной... или я неправ?
Равномерным пределом многочленов на отрезке может быть любая непрерывная функция (теорема Вейерштрасса). Если
![$f\in C^1[-1,1]$ $f\in C^1[-1,1]$](https://dxdy-01.korotkov.co.uk/f/0/c/8/0c8a8e03e6b032f23f53f64a3e0e789782.png)
, то можно добиться, чтобы одновременно

и

(сначала равномерно приблизить

, а потом проинтегрировать, поскольку интегрирование непрерывно). Приближая функции типа

сглаженные в точках излома, можно найти последовательность многочленов

(нулевой многочлен), для которых коэффициент при первой степени

. Наверняка можно явные формулы написать, но думать лень.
-- Вт 2025-12-09 11:41:30 --Собственно, можно через многочлены Чебышёва:
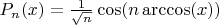
,

нечётно.