Теплоемкость электронного газа (Ландау, Лифшиц)

[palz]

Добрый день.
В книге Ландау и Лифшица "Статистическая физика" (М., 1964) приводится вывод температурной поправки для $\Omega$-потенциала электронного газа (параграф 57, с. 194)
$\Omega=\Omega_0-VT^2\frac{g\sqrt{2\mu}m^{3/2}}{12\hbar^3}$,
где $\Omega_0$ - это значение $\Omega$ - потенциала при абсолютном нуле температуры.
Вводится обозначение $\beta=(g\pi/6)^{2/3}(\frac{m}{\hbar^2})$, где g- спиновая кратность вырождения
Ниже получены выражения для теплоемкости
$ C =\beta NT (V/N)^{2/3}$
и энергии электронного газа
$E=E_0+\frac{\beta}{2}NT^2(V/N)^{2/3}$
Если используем введенное обозначение для $\beta$, а для хим. потенциала используем его значение при нулевой температуре, как это и делается в книге для свободной энергии и энтропии, то выражение для $\Omega$-потенциала можно будет записать в виде
$\Omega=\Omega_0-\frac{\beta}{2}NT^2(\frac{V}{N})^{2/3}$
Выражение для теплоемкости электронного газа известно и такое же указывается, например, в книге Ашкрофта и Мермина "Физика твердого тела". Видно что выражение для полной энергии соответствует этому выражению для теплоемкости. Однако есть нюанс - ведь теперь $\Omega$ и E не связаны через коэффициент (-2/3), а должны - это выводится
в параграфе 55 (см. формулы (55.6) и (55.7)). Согласно этим выражениям $\Omega=-\frac{2}{3}E$. Неясно что за и откуда берется такая нестыковка.

[Cos(x-pi/2)]

Мда... Похоже, что в ЛЛ в параграфе про теплоёмкость вырожденного электронного газа допущена ошибка в формуле для $\Omega.$ Издания 1964 года я не видел, но в издании 1976 года "Статистическая физика, часть 1" (том 5) тоже написана формула, которая при замене в члене с $T^2$ химпотенциала $\mu$ на $\varepsilon_F$ сводится к ошибочной формуле (хотя именно в таком виде она там и не написана) вида

$\Omega=\Omega_0-\frac{\beta}{2}NT^2(\frac{V}{N})^{2/3}$

где $\Omega_0$ это $\Omega$ при нулевой температуре.

Происхождение этой формулы в ЛЛ поясняется с помощью приближённого выражения для интеграла вида

$$I=\int_0^{\infty}\frac{f(\varepsilon)\,d\varepsilon}{e^{(\varepsilon -\mu)/T}+1}$$

Вот приближённое выражение для $I:$

$$I=\int_0^{\mu}f(\varepsilon)\,d\varepsilon\,+\,\frac{\pi^2}{6}T^2f'(\mu)\,+\,...$$

В книге ЛЛ написано, что температурная поправка к $\Omega_0$ получена подстановкой в эту формулу $f(\varepsilon)=\varepsilon^{3/2}.$ Написанное в книге слагаемое с $T^2$ в потенциале $\Omega$ действительно получается из слагаемого с $T^2$ в этом приближённом выражении. Но ведь есть ещё и первое слагаемое, с интегралом.

Слагаемое с интегралом даёт $\frac{2}{5}\mu^{5/2},$ а химпотенциал $\mu$ сам зависит от температуры, так что зависящая от $T$ поправка от $\frac{2}{5}\mu^{5/2}$ тоже даст вклад в $\Omega$ (в книге этот вклад потерян). Зависимость химпотенциала от температуры можно найти из условия постоянства $N/V,$ полагая, что эта величина не зависит от температуры; вычисление здесь аналогичное - с помощью приближённой формулы для интеграла $I,$ в котором в роли функции $f$ теперь будет $\varepsilon^{1/2}.$ Результат:

$$\mu \approx \varepsilon_F\,\left( 1-\frac{\pi^2}{12}\,\frac{T^2}{\varepsilon_F^2}\right)$$

Тогда в итоге получается

$$\Omega=\Omega_0-\frac{\beta}{3}NT^2\left(\frac{V}{N}\right)^{2/3}$$

и равенство $\frac{2}{3}E=-\Omega$ выполняется.

[pppppppo_98]

Cos(x-pi/2) в сообщении #1711790 писал(а):

химпотенциал $\mu$ сам зависит от температуры, так что зависящая от $T$ поправка от $\frac{2}{5}\mu^{5/2}$ тоже даст вклад в $\Omega$ (в книге этот вклад потерян)

Это большой канонический ансамбль. Потенциал $\Omega=-P V$ является функцией трех независимых переменных $\mu, T, V$... 37 стих (по памяти) пятой книги бытия... Никаких иных поправок быть не должно.

-- Пн дек 08, 2025 01:14:20 --

Cos(x-pi/2) в сообщении #1711790 писал(а):

Зависимость химпотенциала от температуры можно найти из условия постоянства $N/V,$ полагая, что эта величина не зависит от температуры

Тогда это просто канонический ансамбль, и для него потенциал $F=\Omega + N \mu$, и зависит он от $N,V,T$

[Cos(x-pi/2)]

pppppppo_98

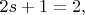
В итоговых результатах в книге бытия всё выражено через заданные $N,V,T.$ Но промежуточная формула, из-за которой у ТС возник вопрос, содержит $\mu$ (ниже пишу всё для электронов, т.е. со "спиновой двойкой" $2s+1=2,$ как и в ЛЛ-5):

$\Omega=\Omega_0-T^2\frac{\sqrt{2\mu}m^{3/2}V}{6\hbar^3}$

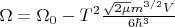
Эта формула приведена в пятой книге бытия, стих 58 "Теплоёмкость вырожденного электронного газа". И прямо под этой формулой там напечатано: "Посредством $\Omega_0$ обозначена величина $\Omega$ при абсолютном нуле температуры."

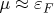
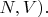
На мой взгляд, это очень корявое место. Оно, возможно, и не ошибочное, если применять такое слагаемое с $T^2$ из $\Omega$ только как "малую добавку" в теореме о малых добавках из стиха 24 для написания добавки к $F_0$ (авторы так и делают, подставляя в эту малую добавку $\mu \approx \varepsilon_F$ и выражая энергию Ферми $\varepsilon_F$ через $N,V).$ Но сходу это совсем не очевидно.

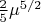
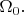
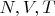
И оно не только не очевидно, а даже не верно, если понимать напечатанное буквально. Потому что получается, что не выписанное авторами явно слагаемое с $\frac{2}{5}\mu^{5/2}$ включено в $\Omega_0.$ Но при заданных $N,V,T$ химпотенциал $\mu$ зависит от $T,$ и тогда зависящая от $\mu$ величина $\Omega_0$ не может быть "величиной $\Omega$ при абсолютном нуле температуры" (как утверждают авторы).

Начинают-то вывод $\Omega$ авторы раньше - в стихе 56. Притом вполне понятно начинают - с выражения, верного при любой температуре, которое можно представить так:

$$\Omega=-\frac{2}{3}\,E$$

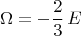
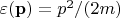
где (через $g(\varepsilon)$ я обозначаю плотность одноэлектронных состояний с энергией $\varepsilon(\mathbf{p})=p^2/(2m)$ и с обеими проекциями спина, она пропорциональна $\varepsilon^{1/2})$

$$E=\int_0^{\infty} \frac{\varepsilon\,g(\varepsilon)\,d\varepsilon}{e^{(\varepsilon -\mu)/T}+1}}\,=\,\frac{\sqrt{2}m^{3/2}V}{\pi^2\hbar^3}\,I$$

$$I\,=\,\int_0^{\infty}\frac{\varepsilon^{3/2}\,d\varepsilon}{e^{(\varepsilon -\mu)/T}+1}\,\approx \,\frac{2}{5}\,\mu^{5/2}\,+\,T^2\,\frac{\pi^2}{4}\,\mu^{1/2} \qquad \text{при }\,T/\mu\ll 1$$

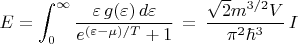
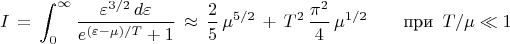
На мой взгляд, если прямо так и довести это вычисление до конца, то всё выглядит понятнее. Ниже изложил это подробнее, может быть топикстартеру пригодится:

Пишем выражение для числа частиц, аналогичное по своему построению указанному выше выражению для энергии системы $E$:

$$N=\int_0^{\infty} \frac{g(\varepsilon)\,d\varepsilon}{e^{(\varepsilon -\mu)/T}+1}}=\frac{\sqrt{2}m^{3/2}V}{\pi^2\hbar^3}\,I_1\,,$$

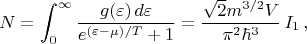
где

$$I_1=\int_0^{\infty}\frac{\varepsilon^{1/2}\,d\varepsilon}{e^{(\varepsilon -\mu)/T}+1}\,\approx\, \frac{2}{3}\,\mu^{3/2}\,+\,T^2\,\frac{\pi^2}{12}\,\mu^{-1/2}$$

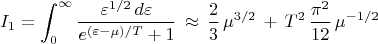
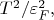
Отсюда, удерживая слагаемые порядка не выше $T^2/\varepsilon_F^2,$ получаем

$$\mu \approx \varepsilon_F\,\left( 1-\frac{\pi^2}{12}\,\frac{T^2}{\varepsilon_F^2}\right)\,,$$

где $\varepsilon_F$ это $\mu$ при $T=0,$ т.е. энергия Ферми определяется из равенства

$$N=\int_0^{\varepsilon_F}d\varepsilon\,g(\varepsilon)\,=\,\frac{\sqrt{2}m^{3/2}V}{\pi^2\hbar^3}\,\frac{2}{3}\,\varepsilon_F^{3/2}$$

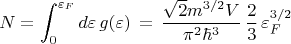
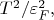
В результате, удерживая везде слагаемые только порядка не выше $T^2/\varepsilon_F^2,$ приходим к выражению для энергии электронного газа (в стихе 58 оно появляется в самом конце):

$$E=E_0+\frac{\beta}{2}NT^2(V/N)^{2/3}\,,$$

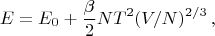
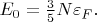
где $E_0=\frac{3}{5}N\varepsilon_F.$ И тем самым автоматически имеем правильное выражение для потенциала $\Omega$ как функции от $N,V,T:$

$$\Omega=-\frac{2}{3}\,E \,= \,\Omega_0 - \frac{\beta}{3}NT^2(V/N)^{2/3}$$

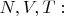
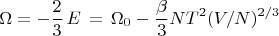
вместо неявно зависящего от $\mu$ выражения, напечатанного в ЛЛ-5, вызвавшего вопрос у ТС.

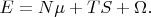
Энтропию $S$ теперь нетрудно найти из имеющегося в стихе 56 равенства $E=N\mu+TS+\Omega.$ С указанной выше точностью получается тот же ответ, что и в стихе 58:

$$S=\beta TN(V/N)^{2/3}$$

Для свободной энергии $F=E-TS$ тоже получается приведённый в стихе 58 ответ:

$$F=F_0 - \frac{\beta}{2}NT^2(V/N)^{2/3}$$

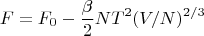
И с теплоёмкостью всё ok:

$$C=\frac{\partial E}{\partial T} = \beta TN(V/N)^{2/3} \,= \,T \,\frac{\pi^2}{3}\,g(\varepsilon_F)$$

[DimaM]

Cos(x-pi/2)
Все так.

palz
Гляньте еще методичку Коткин Г.Л., Лекции по статистической физике. Там может быть проще, чем в Ландавшице.

[Semenych]

В книге Ашкрофта и Мермина и в выражении для энергии используется $\beta/2$ (коэффициент $\pi^2/6$)
Если ты подставишь $\mu=\mu_0$ в формулу для $\Omega$, то получишь коэффициент $\beta/2$
Но если ты учтеш, что $\mu$ меняется с температурой, то итоговый коэффициент для $\Omega$ станет $\beta/3$ (или $\pi^2/9$), что ровно в $-2/3$ раза отличается от энергии
Нет никакой нестыковки, просто заруби себе на носу что НЕЛЬЗЯ просто заменить $\mu$ на $\mu_0$ в термодинамическом потенциале, не учитывая сдвиг самого уровня Ферми, который дает вклад того же порядка малости ($T^2$)!

[Ende]

Semenych
На этом форуме принято обращаться друг к другу на "вы".