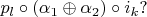Аддитивные и пред-аддитивные категории

[OlgaD]

Я пытаюсь разобраться в структуре аддитивных категорий. Меня интересует аддитивная структура на $hom$-множествах. Если я правильно поняла, сложение двух параллельных морфизмов $f,g:a\to b$ можно определить как композицию следующего вида $a\stackrel{\Delta}{\rightarrow}a\oplus a\stackrel{f\oplus g}{\rightarrow}b\oplus b\stackrel{\nabla}{\rightarrow}b,$ где $\Delta$ - диагональный морфизм, а $\nabla$ - кодиагональный морфизм. В нескольких источниках (и в частности, в Википедии) проскользнуло, что это внутреннее определение суммы морфизмов, обусловенное структурой самой категории. Более того в книге Masaki Kashiwara, Pierre Schapira Categories and Sheaves мне встретилось доказательство теоремы (для пред-аддитивных категорий), утверждающая, что сумма $f+g\in\mathrm{Hom}$ совпадает с этой композицией. То есть есть два альтернативных определения суммы морфизмов, которые приводят к одному и тому же результату? Кажется, я упускаю что-то важное.

[dgwuqtj]

Обычно аддитивные (и предаддитивные) категории — это категории, обогащённые над $\mathbf{Ab}$. То есть для параллельных морфизмов $f, g \colon a \to b$ уже определена сумма $f + g$. Вы хотите проверить, что ваша композиция равна $f + g$, или у вас изначально альтернативное определение аддитивных категорий и нужно построить сложение?

[OlgaD]

Здравствуйте. У меня возник тот же вопрос. Особенно после описания сложения морфизмов здесь: https://en.wikipedia.org/wiki/Additive_ ... dition_law. Я заглянула по ссылке в статью Маклейна Duality for group. Обозначения только в каждом источнике меняются, общепринятых обозначений по-видимому для (ко)диагональных морфизмов нет. Сейчас я себе представляю так: если мы рассматриваем аддитивную категорию, то на ней изначально предполагается как-то заданное сложение морфизмов. 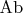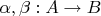Например, в своей статье Маклейн пишет, что в категории абелевых групп $\mathrm{Ab}$ сложение двух морфизмов $\alpha,\beta:A\to B$ задается покомпонентным значением, т.е. 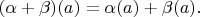$(\alpha+\beta)(a)=\alpha(a)+\beta(a).$ А для категории групп $\mathrm{Grp}$ это сложение может быть выражено через композицию, которую я указала выше. По-видимому, именно эти два способа определения и являются согласованными. Я раньше считала, что имено из-за того, что в (пред)аддитивных категориях появляются бипроизведения, и можно говорить о сложении морфизмов.

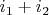
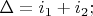
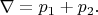
У меня все равно еще остались вопросы. Во-первых, не могу проследить ход мысли в статье Википедии. Сначала определяются (ко)диагональные морфизмы. Это понятно. Но затем они пишут: для каждого объекта $A$ определим сложение инъекций $i_1+i_2$ равным диагональному морфизму, т.е. $\Delta=i_1+i_2;$ а сложение проекций $p_1+p_2$ определеим равным кодиагональному морфизму, т.е. $\nabla=p_1+p_2.$ Мы этого все-таки полагаем или вычисляем? Вроде бы при определении, например, диагонального морфизма мы используем диаграмму произведения, в которой инъекций не наблюдается...

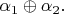
И второй вопрос, я не совсем понимаю как определяется морфизм $\alpha_1\oplus\alpha_2.$ И откуда следует его единственность. И откуда появляеются композиции $p_l\circ(\alpha_1\oplus\alpha_2)\circ i_k?$

[dgwuqtj]

OlgaD в сообщении #1711730 писал(а):

А для категории групп $\mathrm{Grp}$ это сложение может быть выражено через композицию, которую я указала выше.

Эта категория не аддитивная, в ней копроизведение не изоморфно произведению.

OlgaD в сообщении #1711730 писал(а):

По-видимому, именно эти два способа определения и являются согласованными.

Ну да, они дают одно и то же. Мне как-то всегда было проще сначала проверить, есть ли сложение, а потом искать прямые суммы.

OlgaD в сообщении #1711730 писал(а):

в (пред)аддитивных категориях появляются бипроизведения

Нет, в предаддитивных как раз нет произведений, только обогащение над $\mathbf{Ab}$.

OlgaD в сообщении #1711730 писал(а):

Мы этого все-таки полагаем или вычисляем?

Судя по тексту, полагаем. А вообще лучше читайте учебники.

OlgaD в сообщении #1711730 писал(а):

И второй вопрос, я не совсем понимаю как определяется морфизм $\alpha_1\oplus\alpha_2.$

Прямая сумма — это функтор, то есть уже изначально заданы и прямые суммы объектов, и прямые суммы морфизмов. Если у вас прямые суммы даны как бипроизведения, то и произведения, и копроизведения образуют функторы по универсальному свойству.

[OlgaD]

Что значит "полагаем"? Мы уже определили (ко)диагональные морфизмы. Если читать учебник Masaki Kashiwara, Pierre Schapira Categories and Sheaves, то выглядит это так (обозначения оставляю их):

Утверждение. Если $\mathcal{C}$ - пред-аддитивная категория, $X,Y\in\mathcal{C}$ и $f_1,f_2\in\mathrm{Hom}_{\mathcal{C}}(X,Y).$ Предположим, что прямые суммы $X\oplus X$ и $Y\oplus Y.$ Тогда $f_1+f_2\in\mathrm{Hom}_{\mathcal{C}}(X,Y)$ совпадает с композицией

$$X\stackrel{\delta_X}{\rightarrow}X\oplus X\stackrel{f_1\oplus f_2}{\rightarrow}Y\oplus Y\stackrel{\sigma_Y}{\rightarrow}Y.$$

Здесь $\delta_X:X\to X\times X\simeq X\oplus X$ - диагональный морфизм, а $\sigma_Y:Y\oplus Y\simeq Y\sqcup Y\to Y$ - кодиагональный морфизм.

Доказательство. Пусть $i_j:X\to X\oplus X$ и $p_j:X\oplus X\to X$ - $j$-я копроекция и проекция. Тогда мы имеем $p_1\circ (i_1+i_2)=p_1\circ i_1+p_1\circ i_2=\mathrm{id_X}=p_1\circ\delta_X$ и аналогино $p_2\circ(i_1+i_2)=p_2\circ\delta_X.$ Следовательно, мы получаем (!) $i_1+i_2=\delta_X.$ С другой стороны, мы имеем

$$\dsigma_Y\circ(f_1\sqcup f_2)\circ\delta_X=\sigma_Y\circ(f_1\sqcup f_2)\circ(i_1+i_2)=\sigma_U\circ(f_1\sqcup f_2)\circ i_1+\sigma_Y\circ(f_1\sqcup f_2)\circ i_2=f_1+f_2.$$

Я думаю, что равенство $p_1+p_2=\nabla$ тоже можно доказать по двойственности. Но мне совсем не понятно, по какой диаграмме в Википедии строится равенство $p_l\circ(\alpha_1+\alpha_2)\circ i_k=\alpha_k,$ если $k=l,$ и 0 в противном случае. А самое главное, почему этот морфизм единственен.

[dgwuqtj]

В Википедии делают так. С одной стороны, $B \oplus B$ произведение, поэтому существуют $f_1, f_2 \colon A \to B \oplus B$ такие, что $p_i \circ f_i = \alpha_i$ и $p_i \circ f_j = 0$ при $i \neq j$. С другой стороны, $A \oplus A$ копроизведение, поэтому существует морфизм $\alpha_1 \oplus \alpha_2 \colon A \oplus A \to B \oplus B$, для которого $(\alpha_1 \oplus \alpha_2) \circ i_k = f_k$. Единственность проверяется так же.

[OlgaD]

Еще бы "склеить" эти формулы в одну. А как здесь вставляются рисунки?

-- 05.12.2025, 19:47 --

OlgaD в сообщении #1711767 писал(а):

Еще бы "склеить" эти формулы в одну. А как здесь вставляются рисунки?

И потом, $p_i\circ f_i$ не одно и то же, что и $p_i\circ(f_1\oplus f_2).$

[OlgaD]

У меня есть предположение, что морфизм $f_1\oplus f_2:a\oplus a\to b\oplus b$ можно определить либо, рассматривая $b\oplus b$ как произедение, либо рассматривая $a\oplus a$ как копроизведение. Тогда универсальное свойство (ко)произведений гарантирует однозначность морфизма $f_1\oplus f_2.$

[dgwuqtj]

OlgaD в сообщении #1711767 писал(а):

И потом, $p_i\circ f_i$ не одно и то же, что и $p_i\circ(f_1\oplus f_2).$

При чём тут $f_1 \oplus f_2 \colon A \oplus A \to B \oplus B \oplus B \oplus B$? Мы строим $\alpha_1 \oplus \alpha_2$.

[OlgaD]

Здравствуйте. Мы друг друга не поняли. Я думаю, что морфизм $\alpha_1\oplus\alpha_2$ можно определить, например, следующей диаграммой

$$\begin{array}{ccc} a & \stackrel{\alpha_1}{\longrightarrow} & b \\ \uparrow & & \uparrow \\ &&\\ a\oplus a & \stackrel{\alpha_1\oplus\alpha_2}{\longrightarrow} & b\oplus b \\ &&\\ \downarrow & & \downarrow \\ a & \stackrel{\alpha_2}{\longrightarrow} & b \\ \end{array}$$

где вертикальные стрелки с той и с другой стороны --- соответствующие проекции, при этом рассматривая $b\oplus b$ как произведение.

[dgwuqtj]

Ну да, можно и так.

[OlgaD]

Единственно, я не уверена в существовании диагональных морфизмов $a\oplus a\to b.$

[dgwuqtj]

А это тоже следует из универсального свойства произведений. Есть даже такое чуть более общее понятие, декартовы категории.

[OlgaD]

Спасибо, до них я еще не дошла