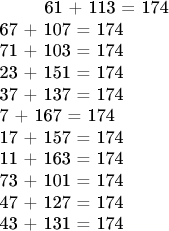Здравствуйте! В этом посте я расскажу о формулах для вычисления примерного количества пар простых чисел, которые в сумме дают N (кратное шести).

Чётное натуральное число

количество уникальных пар составных чисел вида
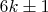
, дающих в сумме N
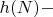
количество уникальных способов представить число

в виде суммы двух простых чисел вида
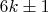
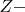
количество уникальных пар, где одно число простое, а другое — составное.
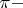
количество простых чисел до N.
Формула 1.
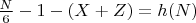
Формула 2.
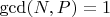
![$\[
X + Z = \sum_{P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1} - a \right)
- 2 \sum_{P_2 > P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1 P_2} \right)
+ \cdots + (-1)^{\pi(\sqrt{N})}2 \sum_{P_o > \cdots > P_2 > P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1 P_2 \cdots P_o} \right)
\]$ $\[
X + Z = \sum_{P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1} - a \right)
- 2 \sum_{P_2 > P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1 P_2} \right)
+ \cdots + (-1)^{\pi(\sqrt{N})}2 \sum_{P_o > \cdots > P_2 > P_1 > 3}^{\sqrt{N}} \left( \frac{N}{3 P_1 P_2 \cdots P_o} \right)
\]$](https://dxdy-02.korotkov.co.uk/f/d/a/6/da6c0bb7bd77aade0ca650a743a79c0282.png)
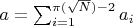
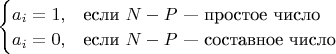
Примеры.
N=174
![$X + Z =\[
\frac{174}{3 \times 5} + \frac{174}{3 \times 7} + \frac{174}{3 \times 11} + \frac{174}{3 \times 13} - 2 \left( \frac{174}{3 \times 5 \times 7} + \frac{174}{3 \times 5 \times 11} + \frac{174}{3 \times 5 \times 13} + \frac{174}{3 \times 7 \times 11} + \frac{174}{3 \times 7 \times 13} + \frac{174}{3 \times 11 \times 13} \right) + 2 \left( \frac{174}{3 \times 5 \times 7 \times 11} + \frac{174}{3 \times 5 \times 7 \times 13} + \frac{174}{3 \times 5 \times 11 \times 13} + \frac{174}{3 \times 7 \times 11 \times 13} \right) - \frac{174}{3 \times 5 \times 7 \times 11 \times 13}
\]$ $X + Z =\[
\frac{174}{3 \times 5} + \frac{174}{3 \times 7} + \frac{174}{3 \times 11} + \frac{174}{3 \times 13} - 2 \left( \frac{174}{3 \times 5 \times 7} + \frac{174}{3 \times 5 \times 11} + \frac{174}{3 \times 5 \times 13} + \frac{174}{3 \times 7 \times 11} + \frac{174}{3 \times 7 \times 13} + \frac{174}{3 \times 11 \times 13} \right) + 2 \left( \frac{174}{3 \times 5 \times 7 \times 11} + \frac{174}{3 \times 5 \times 7 \times 13} + \frac{174}{3 \times 5 \times 11 \times 13} + \frac{174}{3 \times 7 \times 11 \times 13} \right) - \frac{174}{3 \times 5 \times 7 \times 11 \times 13}
\]$](https://dxdy-01.korotkov.co.uk/f/0/a/6/0a6e7f12a8bc107756d4b0e3bf88054382.png)
Фактическое число
17
Подставляем значения в формулу 1.
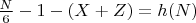
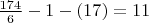
Вывод: количество разложений числа N (174) в сумму двух простых равняется 11.