Доказательство что размерность ФСР = числу свободных членов

[cxzbsdhwert]

Лемма: "Размерность подпространства решений однородной системы линейных уравнений (СЛУ) с $n$ неизвестными равна числу свободных неизвестных". Начало доказательства; конкретная часть, которая непонятна.

Лектор, доказав линейную независимость (л\н) множества из $k$ единиц $n$-мерных векторов, полученных подстановкой в $k$-тый вектор, на места компонент, соответствующих номеру свободных переменных СЛУ, компонент $k$-го вектора из стандартного базиса $\mathbb{R}^k$, а на места остальных компонент что-то ассоциированное с зависимыми переменными (мне не понятно что), перешёл к доказательству того что множество таких векторов не только л\н но и порождает всё подпространство решений данной однородной СЛУ, для того чтобы доказать что это множество векторов базис, а значит фундаментальная система решений (ФСР), а значит размерность определяется числом векторов в такой ФСР, то есть числом свободных переменных ч.т.д.

Доказательство заключается в том, что произвольное решение $(x^{0}_1,...,x^{0}_n)$ СЛУ, может быть выражено как линейная комбинация $k$ вышеописанных векторов с коэффициентами, равными компоненте свободной переменной вектора произвольного решения, соответствующей по номеру, номеру базисного вектора, на который такой коэффициент умножается, то есть:

$$(x^{0}_1,...,x^{0}_n)=x^{0}_{i_1}(x^{1}_1,...,x^{1}_n) + ... + x^{0}_{i_k}(x^{k}_1,...,x^{k}_n)$$

Где $i_k$ - номер компоненты соответствующей свободной переменной. Поскольку их по условию $k$, то от $i_1$ до $i_k$, при этом, как сказал Лектор, $1\leq i_1 < ... < 1_k \leq n$, что кстати тоже не понятно - почему свободная переменная может быть первой, если по методу Гаусса, в улучшенной матрице первым должен быть лидер, который отождествляется с зависимой переменной.

На 35:01 лишен внимания тот факт, что помимо компонент векторов соответствующих свободным переменным, которые в соответствующих векторах правостороннего выражения имеют единичное значение, а в левостороннем векторе некоторое произвольное, в правосторонних векторах, помимо несовпадающих с номером вектора нулевых компонент также соответствующим свободным переменным, есть ещё компоненты соответствующие зависимым переменным, и они могут быть (а наверное и всегда) отнюдь не нулевые, что означает, что они тоже умножаются на компоненту свободной переменной из левого вектора.

Отсюда возникает вопрос о правильности равенства: получается, в векторах ФСР компоненты зависимых переменных равны отношению нужного значения (в соответствии с левосторонним вектором) к умножаемой компоненте свободной переменной, чтобы при умножении на компоненту свободной переменной знаменатель сократился?
Но система же может быть неопределенна, то есть могут быть разные решения, и как следствие, нужное отношение может быть к разным свободным величинам, но тогда один базис подойдёт только для одного решения, а базис по определению должен порождать множество всех решений. Мне тут видится таким образом противоречие.
Где я не прав?

Могу предположить, что зависимые компоненты, при других свободных, будут меняться таким образом, чтобы при умножении всё того же зависимого компонента вектора базиса на новый свободный компонент всё "сходилось", но это по-моему предположение требующее доказательства.

[mihaild]

cxzbsdhwert в сообщении #1710966 писал(а):

Отсюда возникает вопрос о правильности равенства: получается, в векторах ФСР компоненты зависимых переменных равны отношению нужного значения (в соответствии с левосторонним вектором) к умножаемой компоненте свободной переменной, чтобы при умножении на компоненту свободной переменной знаменатель сократился?

Ничего непонятно, какое нужное значение, какое соответствие, какой компоненте, какой знаменатель? Можете написать формулой?

Лектор явно сформулировал следующее утверждение: если у двух решений значения свободных неизвестных совпадают, то и значения главных совпадают (это, конечно, надо доказывать; видимо, доказано где-то ранее). Слева и справа решение. Слева и справа значения свободных неизвестных совпадают. Следовательно, слева и справа значения главных неизвестных тоже совпадают.

[cxzbsdhwert]

mihaild в сообщении #1710969 писал(а):

cxzbsdhwert в сообщении #1710966 писал(а):

Отсюда возникает вопрос о правильности равенства: получается, в векторах ФСР компоненты зависимых переменных равны отношению нужного значения (в соответствии с левосторонним вектором) к умножаемой компоненте свободной переменной, чтобы при умножении на компоненту свободной переменной знаменатель сократился?

Ничего непонятно, какое нужное значение, какое соответствие, какой компоненте, какой знаменатель? Можете написать формулой?

Вопрос в том, как компоненты, соответствующие зависимым переменным произвольного решения $(x^{0}_1,...,x^{0}_n)$, обозначим их множество как $\{x_{j_n},...,x_{j_{n-k}}\}$, становятся равными соответствующим по номеру компонентам из линейной комбинации ФСР, сформированной из $k$ векторов, по принципу, описанному выше, если умножение на каждый вектор такой ФСР делается из расчёта привести в равенство значения только свободные переменные.

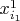
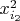
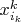
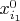
То есть, понятно, что равенство между $x^{0}_{i_1},...,x^{0}_{i_k}$ компонентами сводных переменных произвольного решения и результирующего вектора линейной комбинации ФСР достигается умножением компонент $x^{1}_{i_1}$ первого вектора, $x^{2}_{i_2}$ второго, ..., $x^{k}_{i_k}$ $k$-го из этой линейной комбинации ФСР на $x^{0}_{i_1}$ и т.д. соответственно ($x$ с индексами $i$, напомню, это свободные переменные). Ну, а точнее умножением не отдельных компонент векторов, а всех компонент, включая те, которые в исходном произвольном векторе решений соответствуют зависимым переменным.

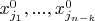
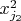
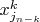
Не понятно как достигается равенство между $x^{0}_{j_1},...,x^{0}_{j_{n-k}}$ компонентами сводных переменных произвольного решения и компонентами $x^{1}_{j_1}$ первого вектора, $x^{2}_{j_2}$ второго, ..., $x^{k}_{j_{n-k}}$ $k$-го из комбинации ФСР (или, в отличии от свободных компонент, которые берутся "по отдельности" из каждого вектора ФСР, комбинацией одной компоненты из нескольких векторов ФСР, умноженных, тогда уже на разные коэффициенты).

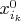
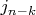
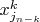
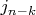
Я предположил, что раз $k$-ый вектор ФСР умножается на $i_k$-ую компоненту вектора произвольного решения $x^{0}_{i_k}$, то $j_{n-k}$-ая компонента $k$-го вектора ФСР $x^{k}_{j_{n-k}}$ необходимая для придания равенства $j_{n-k}$ компоненте вектора произвольного решения $x^{0}_{j_{n-k}}$, которая соответствует зависимой переменной, то такая компонента вектора ФСР должна быть равна $\dfrac{x^{0}_{j_{n-k}}}{x^{0}_k}$, 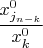а остальных векторов ФСР $j_{n-k}$-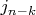ая компонента должна быть нулевой, чтобы при сложении не добавилось лишнего. Например так.
Но проблема в том что базис это конкретные численные значения, и он должен выражать все решения, а получается, что по такой логике, подходит только для одного.

mihaild в сообщении #1710969 писал(а):

Лектор явно сформулировал следующее утверждение: если у двух решений значения свободных неизвестных совпадают, то и значения главных совпадают (это, конечно, надо доказывать; видимо, доказано где-то ранее). Слева и справа решение. Слева и справа значения свободных неизвестных совпадают. Следовательно, слева и справа значения главных неизвестных тоже совпадают.

Да, Он после доказательства это и упомянул, но по-сути, доказательство этого утверждения (о том что если свободные совпадают то и зависимые) и должно быть доказательством, того что такая ФСР выражает остальные решения. И при чём доказательство именно в этом контексте.

То есть буквально, как так будет получаться, что компоненты зависимых переменных ФСР будут совпадать с аналогичными компонентами вектора произвольного решения, при умножении на компоненты свободных переменных вектора произвольного решения, при одном и том же базисе (ФСР).

[mihaild]

cxzbsdhwert в сообщении #1710970 писал(а):

Например так

Нет, так не получится, потому что может оказаться, что какая-то зависимая компонента ненулевая сразу у нескольких векторов ФСР.

cxzbsdhwert в сообщении #1710970 писал(а):

Да, он после доказательства это и упомянул

Это не "после", это и является завершением доказательства.

В 19:37 лектор говорит "переменные разделяются на два типа: на свободные и на главные; свободные - это которые принимают любые значения независимо друг от друга, главные - это которые через них однозначно выражаются". И ссылается при этом, видимо, на предыдущую лекцию.

[cxzbsdhwert]

mihaild в сообщении #1710972 писал(а):

cxzbsdhwert в сообщении #1710970 писал(а):

Например так

Нет, так не получится, потому что может оказаться, что какая-то зависимая компонента ненулевая сразу у нескольких векторов ФСР.

Нет, подобно свободным, каждая зависящая компонента будет только в одном векторе ФСР, а у остальных на её месте нули. Но тут проблема в том что векторов в ФСР $k$, что соответствует числу свободных переменных, а зависимых $n-k$, что может быть больше $k$ (может же?). Но тогда просто несколько векторов будут "ютить" несколько зависимых, а на соответствующие компонентах векторов которые их не "ютят", будут нули, так что дважды ничего складываться не будет.

Но перед этим я предложил и вариант, когда зависящая "разделяется" между векторами (по одной и той же компоненте, разумеется), так чтобы суммирование всё-таки было, и с учётом умножения теперь уже на разные коэффициенты (поскольку разные части одной зависимой переменной теперь в разных векторах ФСР), давало в сумме целую соответствующую зависимую переменную из вектора произвольного решения.

Но это всё догадки. А хотелось бы понимать как на самом деле.
"Если свободные сходятся то и зависимые сходятся" - хорошо, но это более общая формулировка. А в этом случае, как буквально будет, по какому принципу зависимые будут "подстраиваться"?

[mihaild]

cxzbsdhwert в сообщении #1710973 писал(а):

Нет, подобно свободным, каждая зависящая компонента будет только в одном векторе ФСР, а у остальных на её месте нули.

Так может не получиться.
Рассмотрите систему из одного уравнения $x_1 + x_2 + x_3 = 0$. Пусть свободные переменные $x_1$ и $x_2$. Тогда вектора ФСР $(1, 0, -1)$ и $(0, 1, -1)$.

cxzbsdhwert в сообщении #1710973 писал(а):

"Если свободные сходятся то и зависимые сходятся" - хорошо, но это более общая формулировка. А в этом случае, как буквально будет, по какому принципу зависимые будут "подстраиваться"?

Ну можно так попробовать (хотя это надо отдельно доказывать).
Зависимые переменные выражаются через независимые линейным образом. Например $x_1 = 5 \cdot x_2 + 3 \cdot x_3$. Соответственно когда мы берем вектор ФСР для $x_2$ с коэффициентом $a_2$, мы добавляем к $x_1$ как раз $5 \a_2$ - так что это выражение сохраняется.

[cxzbsdhwert]

mihaild в сообщении #1710976 писал(а):

cxzbsdhwert в сообщении #1710973 писал(а):

Нет, подобно свободным, каждая зависящая компонента будет только в одном векторе ФСР, а у остальных на её месте нули.

Так может не получиться.
Рассмотрите систему из одного уравнения $x_1 + x_2 + x_3 = 0$. Пусть свободные переменные $x_1$ и $x_2$. Тогда вектора ФСР $(1, 0, -1)$ и $(0, 1, -1)$.

Ну вот, тут находит место, как я понимаю, второе предположение о "распределении" зависимой компоненты между векторами ФСР. В данном случае в равных частях. Возможно всегда в равных.

mihaild в сообщении #1710976 писал(а):

Ну можно так попробовать (хотя это надо отдельно доказывать).
Зависимые переменные выражаются через независимые линейным образом. Например $x_1 = 5 \cdot x_2 + 3 \cdot x_3$. Соответственно когда мы берем вектор ФСР для $x_2$ с коэффициентом $a_2$, мы добавляем к $x_1$ как раз $5 \a_2$ - так что это выражение сохраняется.

Почему 52? В связи с чем вообще добавляем? У нас на вектора ФСР умножение скаляра происходит при выражении решения как их линейную комбинацию, а не добавление чего-то.