Корректность симметричной формулы ДПФ для нечетной длины

[MGM]

Вот две фомулы для ДПФ:
$\begin{gathered} {\mathbf{F}}_n^{std} = \sum\limits_{t = - {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-\nulldelimiterspace} 2}}^{{T \mathord{\left/ {\vphantom {T {2 - 1}}} \right. \kern-\nulldelimiterspace} {2 - 1}}} {{\mathbf{f}}_t^{std}{e^{ - \frac{{i2\pi n}}{T}t}}} \hfill \\ {\mathbf{F}}_n^{sim} = \sum\limits_{t = - H}^H {{\mathbf{f}}_t^{sim}{e^{ - \frac{{i2\pi n}}{{2H + 1}}t}}} \hfill \\ \end{gathered} $
Обе они "симметричные" по форме, но разные по содержанию.
Первая - стандартная симметрия, вторая симметричная относительно центра последовательности.
Корректна ли вторая? и можно ли по спектру второй что-то восстановить?
Дело в том, что первая легко получается из классического периодического ДПФ со смешением на пол периода $H$.
То есть мое мнение - что вторая формула нерабочая. Или это заблуждение?

[B@R5uk]

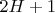
Вообще, первая формула для последовательности с чётным числом T членов, а вторая — с нечётным $2H+1$. Обе одинаково правильные.

-- 29.11.2025, 18:55 --

Отличие обеих формул от стандартной с нумерацией t временных величин от нуля лишь в фазовом множителе, зависящем от номера частоты n. На графике амплитуд частот, где величины берутся по модулю, это даже заметно не будет, потому что эти множители по модулю равны единице.