tsapelЕсли Вы, вместо того чтобы пытаться остроумничать цитатами из Козьмы Пруткова, не поленитесь и почитаете учебники (см. выше ссылку на библиотеку книг по квантовой механике и квантовой теории поля), то, может быть, сами увидите, что вопросы об интенсивности спектральных линий атома (даже самого простого - атома водорода) это очень сложные вопросы.
Случайные события этих 3 излучений равновероятны или какая-то серия более вероятна?
Даже в одной и той же серии спектральные линии различаются интенсивностью. Например, в серии Лаймана чем больше квантовое число

возбуждённого состояния, из которого электрон переходит в основное состояние

тем меньше интенсивность. Она убывает примерно как
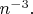
Притом речь здесь идёт лишь о приближённом описании спектра атома водорода, без учёта тонкой и сверхтонкой структуры уровней и радиационных поправок (о таких подробностях на школьных уроках физики, наверное, вообще не упоминают).
Интенсивности линий в следующих сериях (Бальмера, Пашена) тоже разные; и от серии к серии в общем уменьшаются.
Если вероятности разные, то почему?
Выше я уже написал Вам, что в квантовой теории есть полезная формула для вероятности перехода (в упоминавшейся книге Г.Бете это формула для вероятности перехода в дипольном приближении (12.33). Она есть и во многих других учебниках по квантовой теории). Вероятность пропорциональна квадрату модуля матричного элемента перехода, а он зависит от формы волновых функций электрона в начальном и конечном состоянии. И есть ещё очень важный сомножитель в этой формуле - частота излучения

в степени
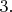
Интенсивность же излучения получается умножением этой вероятности перехода (в единицу времени) на энергию излучаемого кванта

Итого, частота

входит в ответ для интенсивности излучения в степени

Значит, например, для серии Лаймана эта частота в степени

зависит от номера уровня
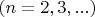
возбуждённого состояния так:
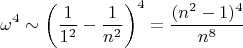
Эта функция с увеличением

не очень сильно возрастает, и при

её значения приближаются к единице. А квадрат модуля матричного элемента это более сложная функция; она, оказывается, быстро убывает с увеличением

(при
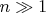
как
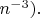
Из-за этого интенсивность линий с увеличением

убывает.
Для серий Бальмера и Пашена матричные элементы разных переходов ведут себя по-своему, так как волновые функции электрона в разных переходах разные и уже не те, что в серии Лаймана. Но тенденция та же: с ростом частоты перехода

матричные элементы убывают. Поскольку

в этих сериях меньше, чем в серии Лаймана, то эти серии оказываются менее интенсивными, чем серия Лаймана.
Вероятности этих излучений постоянны или могут изменяться?
Могут изменяться, поскольку в зависимости от обстоятельств могут изменяться волновые функции электрона (и, значит, матричные элементы переходов), а также сам спектр уровней энергии (и, значит, частоты переходов
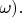
К сказанному выше уважаемым
amon добавлю, что даже в никак не изменённом атоме водорода в сериях Бальмера, Пашена и т.д. возможны разные интенсивности для переходов с заданными начальным

и конечным

Потому что матричные элементы переходов зависят не только от главных квантовых чисел

и

но ещё и от орбитального момента импульса начального и конечного состояний

и

(а частота

в рассматриваемом приближении не зависит от этих квантовых чисел, она зависит только от главных квантовых чисел:
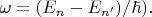
Например, в серии Бальмера не запрещёнными правилами отбора переходами с уровня

на уровень
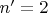
являются переходы между следующими состояниями:
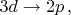
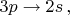
и
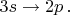
Частота переходов

здесь одна и та же, т.е. речь об одной и той же спектральной линии, типа
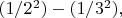
а интенсивность у этих трёх переходов, как показывают расчёты матричных элементов, различается в разы.
Другими словами говоря, интенсивность перехода зависит не только от энергии начального и конечного состояния, но при наличии вырождения ещё и от вида волновой функции возбуждённого состояния на данном уровне энергии (и от вида волновой функции конечного состояния):
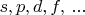
Если вероятности излучений могут меняться, то из-за каких условий?
Из-за любых условий, которые влияют на спектр энергетических уровней и на форму волновых функций атомов. В том числе, при соединении атомов в молекулы изменяются и спектр уровней энергии и волновые функции. Кроме того, можно всё это изменять в той или иной мере внешними полями. Изменение спектра под действием магнитного поля - это так называемый эффект Зеемана; а под действием электрического поля - эффект Штарка. Кроме того, речь пока шла только о спонтанных переходах; в присутствии же переменного электромагнитного поля возникают вынужденные переходы, т.е. вероятность излучения кванта с заданной частотой, волновым вектором и поляризацией увеличивается, если точно такие кванты в объёме с возбуждёнными атомами уже есть; этот эффект применяется в лазерах.
Этот вопрос задали киндеру в школе.
А неважно где и кому задали этот вопрос. Не существует "детской" или "школьной" квантовой механики; которая отвечала бы на любые вопросы языком, доступным для любых киндеров. Есть просто квантовая теория и квантовая физика. Это очень непростая наука. Как показывает опыт преподавания физики вообще, попытки что-то в этой науке выкинуть, упростить или заменить для детей наглядной картинкой, превращаются во враньё.
Школьнику лучше всего прямо так и сказать: не спеши без подготовки браться за квантовую механику, не забивай себе голову ложными упрощениями. Чтобы разбираться в квантовой физике, школьных знаний недостаточно, надо ещё года три-четыре учиться в ВУЗе - изучить ряд дисциплин из высшей математики, математической физики, теоретической физики, экспериментальной физики. Только тогда (и то - лишь может быть, а не наверняка) появится надежда на некоторое понимание.