Пределы комплексного логарифма

[KVV]

Как известно функция комплексного переменного $\exp z$ нигде на расширенной комплексной плоскости не обращается в $0$ или в $\infty$. При $|z|\to\infty$ нет и предела - формально функция стремится к нулю, бесконечности в зависимости от пути, но однозначного предела нет и потому считается, что $\infty$ - существенная особая точка экспоненты $\exp z$.

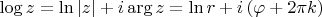
Соответственно обратная экспоненте функция комплексного логарифма $\log z = \ln |z| + i \arg z = \ln r + i\left(\varphi +2\pi k\right)$ не имеет определенных значений в $0$ и в $\infty$ - точки разветвления (branch points). Но имеет ли комплексный логарифм пределы в этих точках? Верно ли, можем ли мы сказать, что

$$\lim_{|z|\to 0} \log z = \infty$$

,

$$\lim_{|z|\to \infty} \log z = \infty$$

?

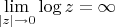
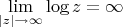
Или, что эквивалентно, можно взять функцию $\exp 1/z$ с существенной особой точкой в нуле и обратную ей $\frac{1}{\log z}$, и рассмотреть следующие пределы:

$$\lim_{|z|\to 0} \frac{1}{\log z} = 0$$

,

$$\lim_{|z|\to \infty} \frac{1}{\log z} = 0$$

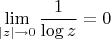
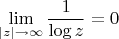
. Корректны ли они? Что об этом говорит ТФКП?

[dgwuqtj]

На логарифм надо смотреть как на функцию $\mathbb C^* \to \mathbb C / 2 \pi i \mathbb Z$, чтобы оно было обычным отображением, а не многозначным. Область значений $\mathbb C / 2 \pi i \mathbb Z$ является открытым цилиндром, его можно вложить в компакт $[-\infty, +\infty] \times (\mathbb R / 2 \pi \mathbb Z)$ (замкнутый цилиндр). После вложения множество предельных точек $\log z$ при $z \to 0$ — это вся окружность $\{-\infty\} \times (\mathbb R / 2 \pi \mathbb Z)$, а при $z \to +\infty$ — похожая окружность с $+\infty$. То есть обычных пределов нет.

С другой стороны, можно вложить в другой компакт, склеив эти окружности в точки $-\infty$ и $+\infty$, топологически получится сфера. Тогда пределы будут $\pm \infty$.

[KVV]

dgwuqtj
Тогда уж лучше склеить обе окружности в одну так, чтобы получился тор, потому как в ТФКП обычно не делают различия между $-\infty$ и $+\infty$. Это просто одна точка $\infty$ - северный полюс сферы Римана. Насколько я понял, вы скорее согласны с тем, что пределы существуют?

Наверняка кто-то иначе считает?

[dgwuqtj]

Они существуют в зависимости от того, куда действует логарифм.