В попытке доказать гипотезу Гольдбаха

[kukonkov]

Здравствуйте. В этом посте я не буду не чего доказывать, лишь поделюсь формулами, которые получил, в попытке доказать гипотезу Гольдбаха. Формулы проверены мной в питоне , если кто хочет сам может всё проверить. Если кого заинтересует та, или иная формула , я расскажу, как она была выведена и, как она может быть использована. С. Ферматист. Куконков Евгений - (Хобен).

**Анализ числовых представлений.**

Куконков Евгений Алексеевич.

Связь $\( x, z, h(N) \)$.

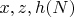
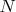
- $\( N \)$ — чётное натуральное число
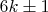
- $\( x \)$ — количество уникальных пар составных чисел вида $\( 6k \pm 1 \)$, дающих в сумме $\( N \)$
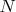
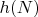
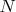
- $\( h(N) \)$ — количество уникальных способов представить число $\( N \)$ в виде суммы двух простых чисел вида \( 6k \pm 1 \)
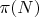
- $\( \pi(N) \)$ — количество простых чисел до $\( N \)$
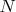
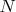
- $\( z \)$ — количество уникальных способов представить число $\( N \)$ в виде суммы одного простого и одного составного чисел

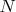
Для чётных чисел $\( N \)$, кратных 6, справедливы следующие формулы:

---

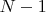
**При $\( N-1 \)$ составном:**

$\[ \text{Формула 1.1.} \quad x - \left( \frac{N}{6} - 1 - (\pi(N) - 2) \right) = h(N) \]$

$\[ \text{Формула 1.2.} \quad \frac{N}{6} - 1 - (X + z) = h(N) \]$

$\[ \text{Формула 1.3.} \quad \frac{N}{3} - 1 - (\pi(N) - 2) = 2X + Z \]$

$\[ \text{Формула 1.4.} \quad \pi(N) - 2 = 2h(N) + 1 + Z \]$

---

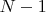
**При $\( N-1 \)$ простом:**

$\[ \text{Формула 2.1.} \quad x - \left( \frac{N}{6} - (\pi(N) - 2) \right) = h(N) \]$

$\[ \text{Формула 2.2.} \quad \frac{N}{6} - (X + z) = h(N) \]$

$\[ \text{Формула 2.3.} \quad \frac{N}{3} - 1 - (\pi(N) - 2) = 2X + 1 + Z \]$

$\[ \text{Формула 2.4.} \quad \pi(N) - 2 = 2 \phi(N) + Z \]$

---

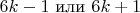
**Количества пар составных чисел вида $\( 6k - 1 \) или \( 6k + 1 \)$, в которых одно слагаемо делится на $\( P \)$:**

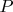
$\[ \gcd(N, P) = 1 \]$

$\[ \text{Формула 3.1.} \quad \frac{N}{3P} - 1 - \frac{\pi(N)}{P-1} - c \]$

$\[ \text{При } \gcd(N, P) = P: \quad \text{Формула 3.2.} \quad \frac{N}{6P} - 1 \]$

---

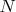
**Для чётных чисел $\( N \)$, не кратных 6, справедливы следующие формулы:**

Дополнительные обозначения:

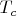
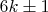
- $\( T_c \)$ — количество составных чисел вида $\( 6k \pm 1 \)$, не участвующих в образовании пар
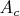
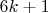
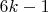
- $\( A_c \)$ — превышение количества составных чисел вида $\( 6k + 1 \)$ над количеством составных чисел вида $\( 6k - 1 \)$ на интервале $\([1, N]\)$
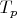
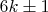
- $\( T_p \)$ — количество простых чисел вида $\( 6k \pm 1 \)$, не участвующих в образовании пар
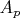
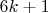
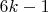
- $\( A_p \)$ — превышение количества простых чисел вида $\( 6k + 1 \)$ над количеством простых чисел вида $\( 6k - 1 \)$ на интервале $\([1, N]\)$
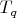
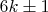
- $\( T_q \)$ — количество простых чисел вида $\( 6k \pm 1 \)$, участвующих в образовании пар

**Примерная оценка (погрешность не более 2):**

$\[ \text{Формула 4.1.1.} \quad \left( \frac{N}{3} - 1 \right) \times \frac{3}{4} - (\pi(N) - 2) = x + T_c - h(N) \]$

$\[ \text{Формула 4.1.2.} \quad \frac{\left( \frac{N}{3} - 1 \right)}{4} - (\pi(N) - 2) = x - T_p - h(N) \]$

$\[ \text{Формула 4.2.1.} \quad \frac{\left( \frac{N}{3} - 1 \right)}{4} - (x + z) = h(N) \]$

$\[ \text{Формула 4.2.2.} \quad \left( \frac{N}{3} - 1 \right) - (\pi(N) - 2) = 2x + z + T_c \]$

$\[ \text{Формула 4.2.3.} \quad (\pi(N) - 2) = 2 \phi(N) + Z + T_p \]$

Подформулы 4.3–4.6:

$\[ \textbf{T}_c = \begin{cases} \frac{\left[\frac{N}{3} - 1\right] - (\pi(N) - 2)}{2} - \frac{A_c}{2}, & \text{если } N \bmod 6 = 2 \\ \frac{\left[\frac{N}{3} - 1\right] - (\pi(N) - 2)}{2} + \frac{A_c}{2}, & \text{если } N \bmod 6 = 4 \end{cases} \]$

$\[ \textbf{T}_p = \begin{cases} \frac{(\pi(N) - 2)}{2} - \frac{A_p}{2}, & \text{если } N \bmod 6 = 2 \\ \frac{\pi(N) + 2}{2} + \frac{A_p}{2}, & \text{если } N \bmod 6 = 4 \end{cases} \]$

---

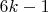
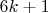
**Количество пар составных чисел вида $\( 6k - 1 \)$ или $\( 6k + 1 \)$, в которых одно слагаемо делится на $\( P \)$:**

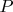
$\[ \gcd(N, P) = 1 \]$

$\[ \text{Формула 5.1.} \quad \frac{N}{6 P} - 1 - \frac{T_q}{P - 1} - c \]$

$\[ \text{При } \gcd(N, P) = P: \quad \text{Формула 5.2.} \quad \frac{N}{12 P} - 1 \]$

[SerjeyMinsk]

Формулы 4.x содержат величины T_c, T_p, A_c, A_p, которые сами зависят от $h(N)$. Это создаёт круговую зависимость: чтобы найти $h(N)$, нужно знать распределение простых, что не проще оригинальной задачи.

[kukonkov]

SerjeyMinsk
Так, я же не заявлял то, что именно с помощью их можно доказать гипотезу Гольдбаха. Просто интересные факты. Да , ранее я пытался вычислить X, но сейчас до меня дошло, как можно проще, вычислив (X+Z), найти h(N). Сейчас я дорабатываю несколько моментов, но могу сказать , по моему скромному мнению, что возможно, зная лишь N и простые до некоторого заданного числа, найти (X+Z).

[SerjeyMinsk]

Вам не нужен критик. Вам нужен проповедник, который скажет: "Да, ваши интересные факты — это наука". Удачи в мире "возможно" и "вероятно"!

[kukonkov]

SerjeyMinsk
я не претендую на звание математика, да меня даже сложно назвать любителем.
я просто вывел формулы и решил поделится ими (я не встречал раньше их и попытка их прогуглить, также оказалась , обреченной на провал.)
Удачи в мире "возможно" и "вероятно"!-хм, я же употребил слово "возможно", не в контексте строгого доказательства, а лишь в описании своей мотивации, Или, что слово можно, математики и в повседневном разговоре возводят в табу.

[kukonkov]

SerjeyMinsk
Попробую принять критику, и строго на неё ответить.
Да , вы правы что Формулы 4.x содержат величины T_c, T_p, A_c, A_p, которые сами зависят от $h(N)$.
Но, для поставленной задачи, достаточно знать, что они больше нуля.
Исходя из формулы 4,1,1,
Мы имеем, то что :
если значение X находится в пределах (N/12, N/6), то что я доказываю (не в этом посте), тогда h(N)>0, независимо от величин T_c, T_p, A_c, A_p,
они необходимы лишь для точного подсчёта количества.