Given a triangle
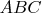
with orthocenter

, altitude

, and median
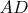
. A line segment

is parallel to
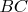
such that

lies on the circumcircle

of
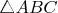
and
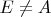
. Let

(
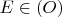
and
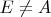
.
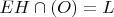
;
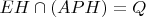
, where

is the foot of the perpendicular from

to
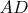
.
Prove that:

, where

is the midpoint of

Oh, it seems a little bit difficult to upload an image on this forum.
Even though I know how to solve it but I think my auxiliary line is kinda unnatural. And I want other's very first idea to solve this such problem.
Btw, my solution is let

such that
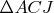
is acute at

and similar to
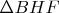
and
