Пусть
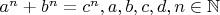
.
Пусть
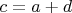
, тогда
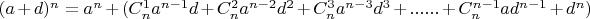
. Очевидно скобка должна быть равна

, т.е. должно выполняться равенство:
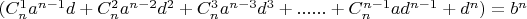
. Назовем оболочкой гиперкуба

, дополняющей его до гиперкуба

величину, равную
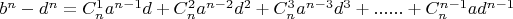
. Почему величина
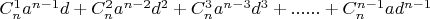
не может быть оболочкой гиперкуба

, дополняющей его до гиперкуба

? И в принципе может ли оно быть оболочкой хоть какого-то целочисленного n-куба?