Вопрос по теореме Эйлера

[Dedekind]

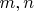
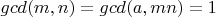
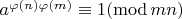
Задача: для любых целых $a$ и любых целых положительных $m, n$ доказать, что если $gcd(m, n) = gcd(a, mn) = 1$, то $a^{\varphi(n)\varphi(m)} \equiv 1 (\operatorname{mod} mn)$. Тут $\varphi$ - функция Эйлера.

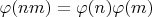
Можно доказать через мультипликативность функции Эйлера: $\varphi(nm)=\varphi(n)\varphi(m)$. Но кажется, можно и проще. Проверьте, пожалуйста, нет ли ошибки.

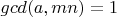
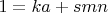
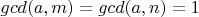
Поскольку $gcd(a, mn) = 1$, то $1 = ka + smn$. Отсюда следует, что $gcd(a, m) =gcd(a, n)= 1$. Следовательно, по теореме Эйлера: $a^{\varphi(n)} \equiv 1 (\operatorname{mod} n)$.
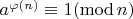
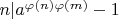
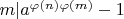
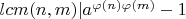
Возводя обе части в степень $\varphi(m)$, получаем $a^{\varphi(n)\varphi(m)} \equiv 1 (\operatorname{mod} n)$. Аналогично получим $a^{\varphi(n)\varphi(m)} \equiv 1 (\operatorname{mod} m)$. Следовательно, $n|a^{\varphi(n)\varphi(m)}-1 $ и $m|a^{\varphi(n)\varphi(m)}-1$. Из этого следует, что $lcm(n, m) | a^{\varphi(n)\varphi(m)}-1$, а поскольку $n$ и $m$ взаимно просты, то $mn|a^{\varphi(n)\varphi(m)}-1$.
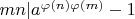
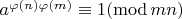
Тогда $a^{\varphi(n)\varphi(m)} \equiv 1 (\operatorname{mod} mn)$, что и требовалось доказать.

[nnosipov]

Dedekind в сообщении #1708265 писал(а):

Можно доказать через мультипликативность функции Эйлера: $\varphi(nm)=\varphi(n)\varphi(m)$.

Зачем? Здесь все очевидно: доказываем сравнение отдельно для каждого из модулей $m$, $n$, опираясь на теорему Эйлера.

Посмотрел Ваш текст: ну да, ровно это я и имел в виду.

[Dedekind]

nnosipov
Спасибо!