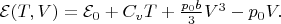Уравнение адиабаты

[Ascold]

Требуется вывести уравнение адиабаты для некоторого вещества с уравнением состояния

$$p=p_0\left(1+aVT-bV^2\right),$$

где $p_0,a,b$ - постоянные величины. Мне кажется, без указания, как зависит внутренняя энергия этого вещества от макропараметров, это невозможно сделать, я прав или нет?

[lel0lel]

На всякий случай замечу, что изотермы весьма причудливы, занимаемый системой объём ограничен сверху. Не приходит в голову кому бы такое могло принадлежать, уж явно не газ. С другой стороны, сейчас стало модно привлекать термодинамику к исследованию самых разнообразных систем. Начиная от экономических моделей (экономические революции -- фазовые переходы) и заканчивая моделями вселенной или настроения народа

Ascold в сообщении #1708248 писал(а):

Мне кажется, без указания, как зависит внутренняя энергия этого вещества от макропараметров, это невозможно сделать, я прав или нет?

Да, правы. Но, при некоторых дополнительных предположениях, получить его можно. Для газа Ван-дер-Ваальса ведь получают внутреннюю энергию. Примерно так:

Число частиц постоянное и равно $N$. Условие непротиворечивости уравнений состояния:

$$\frac{\partial C_v(T,V)}{\partial V}=T\left(\frac{\partial^2 p}{\partial T^2}\right)_V.$$

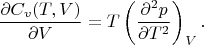
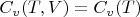
В рассматриваемом случае термическое уравнение линейно по температуре, тогда теплоёмкость в изохорном процессе не зависит от объёма: $C_v(T,V)=C_v(T)$. Чтобы найти внутреннюю энергию $\mathcal{E}(T,V)$ нужно решить следующую систему:
$\begin{cases}\left(\frac{\partial\mathcal{E}}{\partial T}\right)_V&=C_v(T)\\ \left(\frac{\partial\mathcal{E}}{\partial V}\right)_T&=T\left(\frac{\partial p}{\partial T}\right)_V-p\end{cases}$
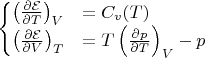
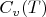
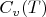
Нужно знать функцию $C_v(T)$. Мы её не знаем, поэтому положим, что в некотором диапазоне теплоёмкость $C_v(T)$ не зависит от $T$. Получится: $\mathcal{E}(T,V)=\mathcal{E}_0+C_v T+\frac{p_0b}{3}V^3-p_0V.$

[dsge]

lel0lel в сообщении #1708300 писал(а):

С другой стороны, сейчас стало модно привлекать термодинамику к исследованию самых разнообразных систем. Начиная от экономических моделей (экономические революции -- фазовые переходы)

В экономике эта мода уже отошла. Физические спекуляции не приносят ни прибыли, ни пользы обществу.

[DimaM]

Ascold
Следуя Румеру-Рывкину, получаем

$$\left(\frac{\partial P}{\partial V}\right)_S=-\frac{T}{C_V}\left(\frac{\partial P}{\partial T}\right)_V^2+\left(\frac{\partial P}{\partial V}\right)_T.$$

То есть да, $C_V$ надо определить, а остальное все считается.

[ozheredov]

lel0lel в сообщении #1708300 писал(а):

сейчас стало модно привлекать термодинамику к исследованию самых разнообразных систем

lel0lel в сообщении #1708300 писал(а):

настроения народа

Подскажите, где почитать?

[lel0lel]

(Оффтоп)

ozheredov, это была не очень удачная шутка. В экономике и космологии примеры найти можно, не всегда удачные.