|
|
Честно говоря определение величины  непонятно, - можете расписать точнее и/или привести численный пример? да, конечно N = 1002 P= 5 Xp = 21 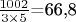 это верхний предел 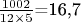 это нижний предел Количество уникальных пар, сумма которых равна 1002: 67 Количество пар с обоими составными числами: 21 Пара: (65, 937) Множители 65: [5, 13] Множители 937: [937] Пара: (97, 905) Множители 97: [97] Множители 905: [5, 181] Пара: (485, 517) Множители 485: [5, 97] Множители 517: [11, 47] Пара: (137, 865) Множители 137: [137] Множители 865: [5, 173] Пара: (295, 707) Множители 295: [5, 59] Множители 707: [7, 101] Пара: (365, 637) Множители 365: [5, 73] Множители 637: [7, 7, 13] Пара: (215, 787) Множители 215: [5, 43] Множители 787: [787] Пара: (247, 755) Множители 247: [13, 19] Множители 755: [5, 151] Пара: (167, 835) Множители 167: [167] Множители 835: [5, 167] Пара: (325, 677) Множители 325: [5, 5, 13] Множители 677: [677] Пара: (397, 605) Множители 397: [397] Множители 605: [5, 11, 11] Пара: (427, 575) Множители 427: [7, 61] Множители 575: [5, 5, 23] Пара: (17, 985) Множители 17: [17] Множители 985: [5, 197] Пара: (175, 827) Множители 175: [5, 5, 7] Множители 827: [827] Пара: (277, 725) Множители 277: [277] Множители 725: [5, 5, 29] Пара: (467, 535) Множители 467: [467] Множители 535: [5, 107] Пара: (127, 875) Множители 127: [127] Множители 875: [5, 5, 5, 7] Пара: (55, 947) Множители 55: [5, 11] Множители 947: [947] Пара: (197, 805) Множители 197: [197] Множители 805: [5, 7, 23] Пара: (245, 757) Множители 245: [5, 7, 7] Множители 757: [757] Пара: (317, 685) Множители 317: [317] Множители 685: [5, 137] Пара: (25, 977) Множители 25: [5, 5] Множители 977: [977] Пара: (475, 527) Множители 475: [5, 5, 19] Множители 527: [17, 31] Пара: (95, 907) Множители 95: [5, 19] Множители 907: [907] Пара: (395, 607) Множители 395: [5, 79] Множители 607: [607] Пара: (47, 955) Множители 47: [47] Множители 955: [5, 191] Пара: (347, 655) Множители 347: [347] Множители 655: [5, 131] Пара: (157, 845) Множители 157: [157] Множители 845: [5, 13, 13] Пара: (457, 545) Множители 457: [457] Множители 545: [5, 109] Пара: (7, 995) Множители 7: [7] Множители 995: [5, 199] Пара: (77, 925) Множители 77: [7, 11] Множители 925: [5, 5, 37] Пара: (235, 767) Множители 235: [5, 47] Множители 767: [13, 59] Пара: (355, 647) Множители 355: [5, 71] Множители 647: [647] Пара: (425, 577) Множители 425: [5, 5, 17] Множители 577: [577] Пара: (497, 505) Множители 497: [7, 71] Множители 505: [5, 101] Пара: (205, 797) Множители 205: [5, 41] Множители 797: [797] Пара: (275, 727) Множители 275: [5, 5, 11] Множители 727: [727] Пара: (307, 695) Множители 307: [307] Множители 695: [5, 139] Пара: (377, 625) Множители 377: [13, 29] Множители 625: [5, 5, 5, 5] Пара: (85, 917) Множители 85: [5, 17] Множители 917: [7, 131] Пара: (227, 775) Множители 227: [227] Множители 775: [5, 5, 31] Пара: (385, 617) Множители 385: [5, 7, 11] Множители 617: [617] Пара: (5, 997) Множители 5: [5] Множители 997: [997] Пара: (125, 877) Множители 125: [5, 5, 5] Множители 877: [877] Пара: (337, 665) Множители 337: [337] Множители 665: [5, 7, 19] Пара: (187, 815) Множители 187: [11, 17] Множители 815: [5, 163] Пара: (155, 847) Множители 155: [5, 31] Множители 847: [7, 11, 11] Пара: (257, 745) Множители 257: [257] Множители 745: [5, 149] Пара: (415, 587) Множители 415: [5, 83] Множители 587: [587] Пара: (37, 965) Множители 37: [37] Множители 965: [5, 193] Пара: (487, 515) Множители 487: [487] Множители 515: [5, 103] Пара: (107, 895) Множители 107: [107] Множители 895: [5, 179] Пара: (265, 737) Множители 265: [5, 53] Множители 737: [11, 67] Пара: (407, 595) Множители 407: [11, 37] Множители 595: [5, 7, 17] Пара: (335, 667) Множители 335: [5, 67] Множители 667: [23, 29] Пара: (455, 547) Множители 455: [5, 7, 13] Множители 547: [547] Пара: (115, 887) Множители 115: [5, 23] Множители 887: [887] Пара: (185, 817) Множители 185: [5, 37] Множители 817: [19, 43] Пара: (305, 697) Множители 305: [5, 61] Множители 697: [17, 41] Пара: (67, 935) Множители 67: [67] Множители 935: [5, 11, 17] Пара: (35, 967) Множители 35: [5, 7] Множители 967: [967] Пара: (367, 635) Множители 367: [367] Множители 635: [5, 127] Пара: (437, 565) Множители 437: [19, 23] Множители 565: [5, 113] Пара: (217, 785) Множители 217: [7, 31] Множители 785: [5, 157] Пара: (145, 857) Множители 145: [5, 29] Множители 857: [857] Пара: (287, 715) Множители 287: [7, 41] Множители 715: [5, 11, 13] Пара: (445, 557) Множители 445: [5, 89] Множители 557: [557]
|
|
01.11.2025, 05:36 
и натурального 
, 
это вот что такое: количество множеств натуральных 
, таких что 
, и 
- составное. 
было составным. Над нижней границей пока не размышлял