Насколько будет эффективен алгоритм поиска простых?

[Altenter]

Здравствуйте, лежу сейчас с ковидом, с температурой 39 и брежу. И набредилась такая идея:
Х. Штаудт в своих исследованиях показал, что частичная сумма обратных простых чисел к номеру числа Бернулли дополняет это число до целого. Будем брать числа Бернулли с номерами $2^n$. Делителями этих номеров будут степени 2. Увеличив эти делители на 1 выберем из них простые числа. Т.е. у чисел Бернулли с номерами $2^N$ сумма обратных простых, дополняющая эти числа до целого, будет состоять из простых чисел вида :$2^n+1$. По сути рекурсивный способ отыскания простых такого вида получится. Если числа Бернулли считать тоже по рекурсии.

Понимаю, что если бы каких-то сложностей не возникало, то этот простой способ уже бы использовали.
В чем будут сложности таких вычислений?

[Altenter]

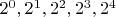
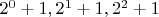
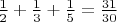
Пример: Возьмем число Бернулли с номером $2^4$. Делителями этого номера будут $2^0, 2^1, 2^2,2^3,2^4$ увеличим эти числа на 1. Допустим мы знаем, что $2^0+1,2^1+1,2^2+1$-простые, а $2^3+1$- составное. Про 2^4+1 мы ничего не знаем и хотим определить, составное оно или простое. 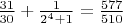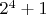Мы берем составляем сумму из обратных простых: $\frac{1}{2}+\frac{1}{3}+\frac{1}{5}=\frac{31}{30}$ добавляем сюда же обратное к нашему неизвестному: $\frac{31}{30}+\frac{1}{2^4+1}=\frac{577}{510}$ теперь смотрим, если эта сумма дополняет само число Бернулли до целого, то $2^4+1$- простое, а если не дополняет, то составное.
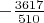
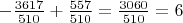
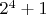
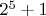
Число Бернулли с номером 16 равно $-\frac{3617}{510}$ прибавляем к нему нашу сумму $-\frac{3617}{510}+\frac{557}{510}=\frac{3060}{510}=6$ т.е. число $2^4+1$- простое. Переходим к числу Бернулли с номером $2^5$ и все повторяем и определяем таким же образом, что число $2^5+1$ составное и так далее по всем числам Бернулли с номерами $2^n$ пока хватит вычислительной мощности.

[dgwuqtj]

Altenter в сообщении #1707424 писал(а):

если эта сумма дополняет само число Бернулли до целого, то $2^4+1$- простое

А это почему? Результат Штаудта, который вы процитировали, про импликацию в другую сторону.

[Altenter]

dgwuqtj в сообщении #1707428 писал(а):

А это почему? Результат Штаудта, который вы процитировали, про импликацию в другую сторону.

Ну я же нашел, что $2^4+1$ простое этим способом. В какую другую? Не понимаю Вас. Может Вы путаете с числами Марена Мерсенна?

-- 28.10.2025, 14:22 --

Если найти простую формулу с малыми вычислительными затратами, которая будет давать сразу числа Бернулли с номерами $2^n$, то этот алгоритм можно было бы использовать для эффективного поиска простых.