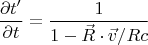Непонятное дифференцирование в ЛЛ-2

[fizGSE]

Здравствуйте!
В ЛЛ-2, издание 1988 года, в параграфе "Потенциалы Лиенара-Вихерта" записано следующее соотношение:

$$\frac {\partial\vec R(t')}{\partial t}=-\vec v(t')$$

Но разве не должно быть:

$$\frac {\partial \vec R(t')}{\partial t}=\frac {\partial( \vec r-\vec r_0(t'))}{\partial t}=-\frac {\partial\vec r_0(t')}{\partial t'}\frac{\partial t'}{\partial t}=-\vec v(t')\frac{\partial t'}{\partial t}\ne-\vec v(t')$$

[Cos(x-pi/2)]

Наверное это просто опечатка: штрих пропущен. Очевидно, по смыслу величины $\vec{R}(t')$ должно быть:

$$\frac {\partial\vec R(t')}{\partial t'}=-\vec v(t')$$

и тогда дальше всё выводится так, как там написано.

[pppppppo_98]

fizGSE в сообщении #1707213 писал(а):

Здравствуйте!
В ЛЛ-2, издание 1988 года, в параграфе "Потенциалы Лиенара-Вихерта" записано следующее соотношение:

$$\frac {\partial\vec R(t')}{\partial t}=-\vec v(t')$$

Но разве не должно быть:

$$\frac {\partial \vec R(t')}{\partial t}=\frac {\partial( \vec r-\vec r_0(t'))}{\partial t}=-\frac {\partial\vec r_0(t')}{\partial t'}\frac{\partial t'}{\partial t}=-\vec v(t')\frac{\partial t'}{\partial t}\ne-\vec v(t')$$

не так
$\frac {\partial \vec R(t')}{\partial t}=\frac {\partial( \vec r-\vec r_0(t'))}{\partial t}=\frac {\partial( \vec r-\vec r_0(t - \frac{R}{c}))}{\partial t}$...Ну и далее по тексту, обратите внимание стоит частная производная по времени t

[Cos(x-pi/2)]

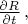
По тексту там вот как, насколько понимаю: в том месте, которое оказалось непонятным топикстартеру, авторы стартуют с рассмотрения производной $\frac {\partial R}{\partial t} \,, $ где:

$$\vec R (t')=\vec r -\vec r_0(t')\qquad (a)$$

$$R\equiv |\vec R(t')|=ct-ct'\qquad (b)$$

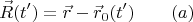
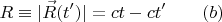
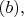
причём $t'$ это решение уравнения $(b),$ т.е. $t'$ зависит от координат и времени произвольной точки наблюдения поля $\vec r$ и $t.$ Авторы пишут сначала очевидное равенство

$$\frac {\partial R}{\partial t}=\frac {\partial R}{\partial t'}\,\frac {\partial t'}{\partial t}\qquad (c)$$

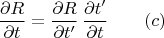
В его левую сторону подставляют выражение, которое сразу получается диференцированием по $t$ левой и правой стороны (b), вот это выражение:

$$\frac {\partial R}{\partial t}=c-c\frac {\partial t'}{\partial t}\qquad (d)$$

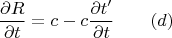
На этом этапе равенство $(c)$ принимает вид

$$c-c\frac {\partial t'}{\partial t}=\frac {\partial R}{\partial t'}\,\frac {\partial t'}{\partial t}\qquad (e)$$

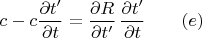
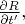
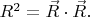
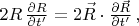
Затем, чтобы найти и подставить сюда $\frac {\partial R}{\partial t'},$ авторы дифференцируют по $t'$ тождество $R^2=\vec R\cdot \vec R.$ Получается: $2R\,\frac {\partial R}{\partial t'}=2\vec R \cdot \frac {\partial \vec R}{\partial t'}\,,$ и отсюда следует, что:

$$\frac {\partial R}{\partial t'}=\frac{1}{R}\,\vec R \cdot \frac {\partial \vec R}{\partial t'}=-\frac{1}{R}\,\vec R \cdot\vec v(t') \qquad (f)$$

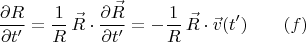
потому что из $(a)$ следует

$$\frac {\partial \vec R}{\partial t'}=-\frac {\partial \vec r_0(t')}{\partial t'}=-\vec v(t')\qquad (g)$$

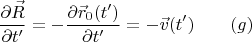
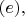
В книге в этом месте опечатка: в левой стороне $(g)$ потерян штрих у переменной $t',$ по которой берётся производная. Ну а затем авторы подставляют $(f)$ в $(e),$ получается равенство

$$c-c\frac {\partial t'}{\partial t}=-\frac{1}{R}\,\vec R \cdot\vec v \, \frac {\partial t'}{\partial t}\qquad (h)$$

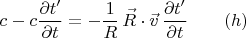
Из него и следует напечатанная далее в книге формула:

$$\frac {\partial t'}{\partial t}=\frac{1}{1-\vec R \cdot\vec v /Rc}$$

[fizGSE]

Спасибо! Значит, буду искать свою ошибку в другом месте.