Надо полагать, что необходимо доказать, что все точки имеют конечный период, тогда нет проблемы найти общий период.
Допустим противное. Пусть

точка с периодом

. Тогда множество
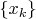

имеет предельную точку

(ваша догадка об использовании компактности будет работать), которая будет непериодической, противоречие, условию, что все точки периодические.
Однако, неочевидно, что функции со свойствами, указанными ТS, существуют.
ну понятно, что задача равносильна тому, что периоды ограничены. однако даже если мы найдём сходящуюся последовательность точек
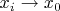
, всё равно непонятно, почему период

должен быть неограничен. идейно мы каждый раз смотрим НОВУЮ функцию, которая сохраняет все

, то есть конечное множество точек. Я не очень понимаю, как такой подхлд можно докрутить непрерывностью((