Винберг Э.Б. "Курс алгебры". Вопросы к книге.

[Altenter]

Ну собственно вот вопрос к § 1 :

Цитата:

Пусть M –– множество с операцией ◦, а N ––множество с операцией ∗. Алгебраические структуры (M, ◦) и (N, ∗) называются изоморфными, если существует такое биективное отображение
f : M → N,
что
f (a ◦ b) = f (a) ∗ f (b)
для любых a, b ∈ M. В этом случае пишут (M, ◦) ≃ (N, ∗). Само отображение f называется изоморфизмом структур (M, ◦) и (N, ∗).

А что, f : M → N,
такое, что
f (a ◦ b) = f (a∗b)

Не будет изоморфизмом? Изоморфизм обязан включать дистрибутивность ?

[dgwuqtj]

Что такое $a * b$? У вас $a, b \in M$, а звёздочка определена на $N$.

[Altenter]

dgwuqtj в сообщении #1706082 писал(а):

Что такое $a * b$? У вас $a, b \in M$, а звёздочка определена на $N$.

Тогда встречный вопрос, что такое у Э.Б. f (a ◦ b) = f (a) ∗ f (b)? Цитата выше.

[Dedekind]

Altenter в сообщении #1706083 писал(а):

что такое у Э.Б. f (a ◦ b) = f (a) ∗ f (b)

Это условие, которому должна удовлетворять $f$, чтобы называться изоморфизмом. При этом, $a, b \in M$, между ними имеет смысл только операция "кружок". $f(a), f(b) \in N$, между ними имеет смысл только операция "звездочка".

[mihaild]

$\circ$ и $*$ - просто функции $M \times M \to M$ и $N \times N \to N$ соответственно, но записываемые в инфиксной записи.
Имеем условие: $f(a \circ b) = f(a) * f(b)$. Подумайте, куда (в $M$ или $N$) входят: $a$, $b$, $a \circ b$, $f(a \circ b)$, $f(a)$, $f(b)$, $f(a) * f(b)$. Проверьте, что всё корректно: $\circ$ применяется к элементам из $M$, $f$ тоже, $*$ - к элементам из $N$ и элементы из $M$ не сравниваются с элементами из $N$.

(а еще прочитайте «Краткий FAQ по тегу [ math]» и набирайте формулы в $\TeX$)

[Altenter]

Спасибо.

-- 16.10.2025, 12:27 --

Изоморфизм - это грубо говоря: $f:M\rightarrow N \cup f(a\circ b)=c\ast d, \forall a,b\in(M,\circ)\cup c,d\in(N,\ast):c=f(a), d=f(b)$, правильно я понимаю?

[Altenter]

Цитата:

Невозможно придумать «из головы» такую систему аксиом, которая привела бы к содержательной теории.

Интересно, из какого места выдумали все существуюшие системы аксиом?)

[Booker48]

Altenter в сообщении #1706097 писал(а):

Цитата:

Невозможно придумать «из головы» такую систему аксиом, которая привела бы к содержательной теории.

Интересно, из какого места выдумали все существуюшие системы аксиом?)

Из осмысления существующей практики, естественно.

[dgwuqtj]

Altenter в сообщении #1706086 писал(а):

Изоморфизм - это грубо говоря: $f:M\rightarrow N \cup f(a\circ b)=c\ast d, \forall a,b\in(M,\circ)\cup c,d\in(N,\ast):c=f(a), d=f(b)$, правильно я понимаю?

Вы почему-то всё время забываете, что $f$ должно быть биекцией. Без этого условия будет определение гомоморфизма.

[Altenter]

dgwuqtj в сообщении #1706099 писал(а):

Altenter в сообщении #1706086 писал(а):

Изоморфизм - это грубо говоря: $f:M\rightarrow N \cup f(a\circ b)=c\ast d, \forall a,b\in(M,\circ)\cup c,d\in(N,\ast):c=f(a), d=f(b)$, правильно я понимаю?

Вы почему-то всё время забываете, что $f$ должно быть биекцией. Без этого условия будет определение гомоморфизма.

Спасибо. Я думал, что $M\rightarrow N$ -это так биекция обозначена, еще хотел спросить, почему не двусторонней стрелкой. Достаточно будет заменить правую стрелку на двустороннюю?

[mihaild]

Altenter в сообщении #1706086 писал(а):

Изоморфизм - это грубо говоря: $f:M\rightarrow N \cup f(a\circ b)=c\ast d, \forall a,b\in(M,\circ)\cup c,d\in(N,\ast):c=f(a), d=f(b)$,

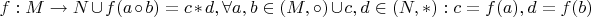
Кроме того, что забыли про биективность, конъюнкция пишется как $\wedge$, и кванторы стоят непонятно как. Дополнительные переменные $c$ и $d$ не нужны.
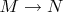
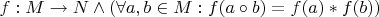
Формулой "$f$ - гомоморфизм $M \to N$" записывается так: $f: M \to N \wedge (\forall a, b \in M: f(a \circ b) = f(a) \ast f(b))$. Обычно домен и кодомен функции пишут отдельно от условий на саму функцию, но это не очень критично.

Altenter в сообщении #1706102 писал(а):

Я думал, что $M\rightarrow N$ -это так биекция обозначена, еще хотел спросить, почему не двусторонней стрелкой

Нет, это обозначение просто фукнции.

Altenter в сообщении #1706102 писал(а):

Достаточно будет заменить правую стрелку на двустороннюю?

Такое обозначение, вроде бы, встречается, но не очень общепринято. Надежнее написать словами.

[Altenter]

mihaild в сообщении #1706105 писал(а):

Такое обозначение, вроде бы, встречается, но не очень общепринято. Надежнее написать словами.

Спасибо.