Задача 3.1 #4.ii из Topology Without Tears

[lebesgspacine]

Найти замыкание множества $\mathbb P$ всех иррациональных чисел в $\mathbb R$.

Я думаю, что $\mathbb P$ всюду плотно, поэтому стал доказывать, что $\bar{\mathbb P} = \mathbb R$.

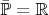
Вот попытка доказательства (от противного):

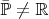
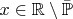
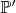
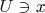
Предположим $\bar{\mathbb P} \not= \mathbb R$. Тогда существует точка $x \in \mathbb R \setminus \bar{\mathbb P}$. Так как $x$ не является элементом $\mathbb P^\prime$, существует открытое множество $U \ni x$, не содержащее иррациональных чисел. Но любое открытое множество в $\mathbb R$ содержит иррациональные числа. Это противоречие. Поэтому $\bar{\mathbb P} = \mathbb R$.

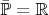
Данное доказательство является ли правильным и достаточно строгим?

[mihaild]

lebesgspacine в сообщении #1706061 писал(а):

Но любое открытое множество в $\mathbb R$ содержит иррациональные числа

Это утверждение нужно доказать.