Ранги произведений равны

[artempalkin]

Это задача из задачника Ким 16.52.2

Путь ненулевая матрица $A\in\mathbb{R}^{n\times n}$ такова, что для любой квадратной матрицы $B$ порядка $n$ выполнено соотношение

$$\operatorname{rg}(AB)=\operatorname{rg}(BA).$$

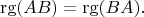
Доказать, что $A$ - невырожденная матрица.

Задача вызвала неожиданную сложность. Рассматривать невырожденную $B$ бесполезно. Пытался составить матрицу $B$ из столбцов ядра $A$ (в предположении, что она вырождена)... но особо не помогает. Наверное, есть какое-то простейшее элегантное решение, что что-то не идет...

[dgwuqtj]

Можно взять $B$ ранга $1$, т.е. вида $B = e f$, где $f$ строка, а $e$ столбец.

А ещё можно домножить $A$ на обратимые матрицы с обеих сторон (что не влияет на утверждение про ранги), чтобы её упростить.

[artempalkin]

dgwuqtj в сообщении #1705982 писал(а):

Можно взять $B$ ранга $1$, т.е. вида $B = e f$, где $f$ строка, а $e$ столбец.

И типа выбрать $e$ из ядра $A$, а $f$ не из ядра $A^T$, правильно я понял?

[svv]

Возьмите в качестве $e$ правый собственный вектор, соответствующий с.з. $\lambda_1$ матрицы $A$, а в качестве $f$ левый собственный вектор, соответствующий с.з. $\lambda_2$:
$Ae=\lambda_1 e, \quad fA=\lambda_2 f$
Тогда из $\operatorname{rg}(AB)=\operatorname{rg}(BA)$ следует
$\operatorname{rg}(\lambda_1 ef)=\operatorname{rg}(\lambda_2 ef)$
Но вдруг $\lambda_1\neq 0, \; \lambda_2=0$? Тогда предыдущее равенство даст $1=0$

[artempalkin]

svv в сообщении #1705989 писал(а):

Возьмите в качестве $e$ правый собственный вектор, соответствующий с.з. $\lambda_1$ матрицы $A$, а в качестве $f$ левый собственный вектор, соответствующий с.з. $\lambda_2$:
$Ae=\lambda_1 e, \quad fA=\lambda_2 f$
Тогда из $\operatorname{rg}(AB)=\operatorname{rg}(BA)$ следует
$\operatorname{rg}(\lambda_1 ef)=\operatorname{rg}(\lambda_2 ef)$
Но вдруг $\lambda_1\neq 0, \; \lambda_2=0$? Тогда предыдущее равенство даст $1=0$

Ну да, в принципе я это и имел в виду, когда говорил

artempalkin в сообщении #1705985 писал(а):

И типа выбрать $e$ из ядра $A$, а $f$ не из ядра $A^T$, правильно я понял?

Правда, что-то я не использую особо выражение "правый/левый собственный вектор", а следовало бы...