А каким критерием интегрируемости Вы пользуетесь? И каким Фихтенгольц? Подозреваю, что у Вас
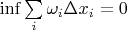
Да, я пользуюсь тем, что

интегрируема на отрезке
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
тттк

существует разбиение (просто разбиение, не размеченное) такое, что
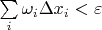
.
Я доказывал так:
Если ограниченная функция

в
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
имеет лишь конечное число точек разрыва, то она интегрируема.
Доказательство:
Пусть точек разрыва у нас

штук. Введем переменную
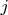
, которая будет пробегать натуральные числа
![$[1, ... , k]$ $[1, ... , k]$](https://dxdy-01.korotkov.co.uk/f/8/c/4/8c4995bcfc8f03938ff22be11ad4f12282.png)
. Если отрезок

покрывает точку разрыва с номером
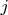
, то
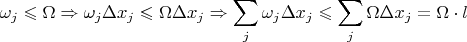
Здесь

- колебание функции на
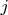
-ом отрезке,

- "глобальное" колебание функции

на всем отрезке
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
,

- суммарная длина отрезков, покрывающие точки разрыва, т.е.
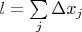
Получается, что если мы хотим, чтобы сумма с колебаниями по отрезкам, покрывающим точки разрыва, была меньше

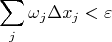
нам достаточно подобрать отрезки так, чтобы
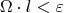
то есть чтобы
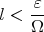
а это, разумеется, можно сделать, т.к. точек разрыва конечное число (и кстати, держа в голове критерий Лебега, то же самое можно было бы сделать, если бы количество точек разрыва имело бы меру 0, но это пока не важно).
С точками разрыва разобрались, переходим к промежуточным отрезкам. Их тоже конечное число, пусть

штук (лень считать сколько точно, потому что точки разрыва еще и на концах отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
могут быть, но это и не важно: не обязательно это

выражать через

, главное что оно конечное). Пусть теперь переменная

пробегает отрезок натуральных чисел
![$[1, ..., p]$ $[1, ..., p]$](https://dxdy-03.korotkov.co.uk/f/6/4/c/64c781517444b87f8de5e9898942781182.png)
.
Возьмем произвольный такой отрезок

. На нем функция непрерывна, поэтому по нашему выбранному в самом начале

найдется

-ое разбиение этого

-ого отрезка (длины отрезков в котром будем обозначать
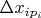
) такое что
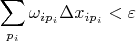
Переводим взгляд на весь отрезок
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
целиком и видим, что мы получили просто какое-то разбиение этого отрезка. Просуммируем все колебания:
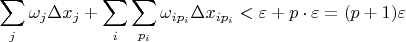
То есть она может быть сделана сколь угодно малой.
Другими словами, для любого

мы смогли сконструировать разбиение отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
такое, что сумма колебаний по этому разбиению меньше, чем
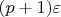
. Что и доказывает теорему.
-- 14.10.2025, 15:07 --А Вы гляньте, ранее по тексту доказан у него этот критерий? Скорее всего он идет позднее. И кстати, там рассуждения похожие, как в док-ве этой теоремы.
Понял, то есть этого критерия у Фихтенгольца пока нету. Кстати, а почему там рассуждения похожие? Этот критерий довольно легко доказывается:

интегрируема на отрезке
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
тттк

существует разбиение такое, что
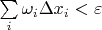
.
Доказательство:
Сначала докажем, что
![$f(x) \in R[a, b] \Rightarrow$ $f(x) \in R[a, b] \Rightarrow$](https://dxdy-02.korotkov.co.uk/f/9/f/6/9f6b1b412bdb37977b897b3f15816e5882.png)

существует разбиение такое, что
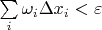
.
Пусть
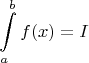
Выберем

-окрестность точки

. По определению интегрируемости, существует

такая, что для любого размеченного разбиения

с параметром

выполняется
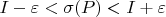
.
Возьмем произвольное такое (пока размеченное) разбиение

.
Тогда если теперь посмотреть на это

не как на размеченное разбиение, а как на просто разбиение, мы увидим, что
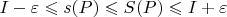
Здесь

и

- соответственно нижняя и верхняя суммы Дарбу, относящиеся к (уже неразмеченному) разбиению

.
А само неравенство выполняется по той причине, что

и

являются соответственно инфимумом и супремумом множества интегральных сумм, соответствующих всем вариантам разметки (неразмеченного и заранее фиксированного) разбиения

.
В итоге получается, что для разбиения


что и требовалось доказать.
В обратную сторону:

существует разбиение такое, что
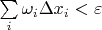
![$\Rightarrow f(x) \in R[a, b]$ $\Rightarrow f(x) \in R[a, b]$](https://dxdy-02.korotkov.co.uk/f/9/4/2/94209286da22831d4781127cf4ec752482.png)
.
Предположим, что левая часть выполняется, а правая - нет. Значит, функция не интегрируема по Риману, следовательно
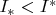
(нижний интеграл Дарбу строго меньше верхнего). Берем произвольное (неразмеченное) разбиение

. Имеем:
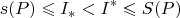
То есть не может разность верхней и нижней сумм Дарбу (она же
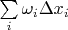
) быть сделанной сколь угодно малой, что вступает в противоречие с левой частью. Чтд.
Тут тоже нету возни с накладывающимися друг на друга отрезками.