Характеристики распределения (в статистике)

[Mihaylo]

Есть такая характеристика распределения - среднее арифметическое. Оно очень часто используется. Есть какие-либо доказательства, что оно самое лучшее из всех? (Критерии "лучшести" неизвестны, вопрос открыт.)

[dsge]

Да, это эффективная статистика, т.е. с наименьшей дисперсией.

[Mihaylo]

Можете изложить как-то теоретическое обоснование? Я не разбираюсь.

P.S. Похоже понял, есть какой-то критерий - минимальность дисперсии. Почему этот критерий лучший?

[dsge]

Mihaylo в сообщении #1705646 писал(а):

Можете изложить как-то теоретическое обоснование? Я не разбираюсь.

P.S. Похоже понял, есть какой-то критерий - минимальность дисперсии. Почему этот критерий лучший?

Это по сути уравнение регрессии с коэффициентом наклона равным 0. Т.е. для регрессии - это BLUE (Best linear Unbiased Estimator). Для метода максимального правдоподобия - это асимптотически эффективная оценка (на самом деле просто эффективная, без асимптотически).

Можно, конечно, привлечь, также, информацию Фишера и критерий Рао-Крамера, но все сведется к вышеуказанному.

[Anton_Peplov]

Mihaylo в сообщении #1705644 писал(а):

Есть такая характеристика распределения - среднее арифметическое. Оно очень часто используется. Есть какие-либо доказательства, что оно самое лучшее из всех?

Среднее арифметическое - это оценка не распределения случайной величины, а ее математического ожидания. Распределение - это функция, ее невозможно оценить одним числом.

Существуют стандартные числовые характеристики (они же моменты) случайной величины $X$: математическое ожидание, дисперсия, момент асимметрии и т.д. Такой параметр распределения $a$ - неслучайная константа. Обычно какой-то интеграл от плотности вероятности.
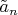
Однако его оценка $\tilde a_n$, вычисляемая по данным $n$ опытов, есть случайная величина. Какое значение она примет, будет зависеть от того, какие значения приняла $X$ в результате опытов.

К оценке обычно применяется следующие требования:

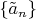
- Состоятельность: последовательность оценок $\{\tilde a_n\}$ (где $n$ - число опытов) должна сходиться по вероятности к истинному параметру $a$. Это самое важное требование.

- Несмещенность: для любого $n$ должно выполняться $M[\tilde a_n] = a$ ($M$ - математическое ожидание), т.е. оценка по крайней мере не имеет тенденции систематически завышать параметр $a$ (или, напротив, систематически занижать его).

- Эффективность: оценка имеет равномерно минимальную дисперсию среди всех состоятельных несмещенных оценок параметра $a$. Ведь при состоятельности и несмещенности чем меньше дисперсия оценки, тем лучше (результаты будут меньше отклоняться от истинного значения $a$). Эффективность оценки зависит от вида закона распределения величины $X$, параметры которого мы оцениваем. Обычно требуют эффективности (или хоть чего-то похожего на неё) для нормального закона.

Среднее арифметическое как оценка математического ожидания величины $X$ - состоятельная, несмещенная, и, для нормально распределенной величины $X$, эффективная. Для других законов распределения она может не быть эффективной.

[Mihaylo]

Допустим мы попытаемся рассмотреть не частный случай - нормальное распределение, а более общий... Что можно сказать про характеристики, оценки? Может быть ничего?

[Anton_Peplov]

Mihaylo в сообщении #1705671 писал(а):

Допустим мы попытаемся рассмотреть не частный случай - нормальное распределение, а более общий... Что можно сказать про характеристики, оценки?

Я уже написал: среднее арифметическое - это состоятельная и несмещенная оценка матожидания при любом распределении.

[Евгений Машеров]

Mihaylo в сообщении #1705644 писал(а):

Есть такая характеристика распределения - среднее арифметическое. Оно очень часто используется. Есть какие-либо доказательства, что оно самое лучшее из всех? (Критерии "лучшести" неизвестны, вопрос открыт.)

Нет, потому, что утверждение неверное. Верное утверждение - с точки зрения некоторых критериев и при определённых условиях оно является оптимальным. Для других критериев это не так.
Среднее арифметическое - несмещённая оценка. В предположении нормальности распределения это максимально правдоподобная оценка. Оно минимизирует сумму квадратов отклонений от элементов выборки. Эти и другие достоинства, вкупе с простотой расчёта среднего, обуславливают его популярность.
Однако оно очень неустойчиво по отношению к выбросам (грубым ошибкам).

(Оффтоп)

Любимый пример - в начале 1990х самые богатые учёные мира работали в Институте Проблем Управления в Москве (если считать среднее состояние). Борис Абрамович Березовский продолжал там числиться завлабом, и его три миллиарда, делённые на тыщу нищих профессоров, давали в среднем три миллиона долларов на человека. Медиана дала бы более грустную оценку.

При иных предположениях о характере распределения оптимальны другие оценки.

[Евгений Машеров]

Среднее арифметическое появилось задолго до развития статистики (вернее, когда под словом "статистика" понималось не цифровое выражение характеристик, а "описание Staat, сиречь государств" - в духе "Государь тамошний вспыльчив, но законы блюдёт, носит длинную бороду и короткий кафтан. Народ же склонен к пьянству и разврату, однако в торговых делах честен"; современная трактовка "статистики" пошла с "Политической арифметики" Вильяма Петти, а математический аппарат сформировался в XIX-XX веках).
Его, среднее арифметическое, использовали для оценки убытков при крушениях кораблей - общая стоимость груза, делённая на число тюков, давала среднюю стоимость тюка, отсюда одно из англоязычных названий этой характеристики - average, от "авария". Достоинство - простота расчёта и аддитивность.
С развитием матстатистики возник вопрос о качестве различных оценок. Были выработаны критерии, которые, однако, могут противоречить друг другу или же вообще не выполняться.
Состоятельность, с содержательной точки зрения, означает, что у нас есть смысл увеличивать объём выборки, по мере роста его - оценка сходится к истинному значению. Но надо заметить, что есть практически важная несостоятельная оценка - периодограммная оценка спектра сигнала. Поскольку по мере увеличения длины отрезка сигнала растёт и число членов разложения Фурье - точность оценки не увеличивается (существуют приёмы обработки данных, позволяющие всё же получить таким путём состоятельную оценку, ценой некоторых потерь - это разбиение сигнала на эпохи и усреднение по эпохам, а также усреднение по частоте). Среднее арифметическое - состоятельная оценка (если существует - считать среднее от величины с распределением Коши занятие несколько медитативное...)
Несмещённость и эффективность практику лучше всего соотнести с понятиями систематической и случайной ошибки (в теории ошибок выделяют ещё грубые). Несмещённая оценка не имеет систематической ошибки, а дисперсия случайной ошибки у эффективных оценок минимальна. Среднее арифметическое - несмещённая оценка (для всех распределений, для которых матожидание существует) и эффективная (для нормального распределения; для других это может быть не так).
Среднее арифметическое естественно возникает при оценке матожидания методом максимального правдоподобия (при нормальности распределения), а также при использовании метода наименьших квадратов. Никуда не делась его вычислительная простота (особенно ярко при расчёте скользящего среднего - пересчёт оценки на очередном шаге сводится к прибавлению значения новой точки, вычитанию значения ушедшей точки и делению на n; медиану можно рассчитать при помощи сортировки n значений, можно сократить алгоритмическими трюками до O(n) операций, но всё равно дольше и сложнее). Ну и "наследство" в виде накопленного опыта.
Но все эти достоинства не исключают того, что среднее может оказаться очень плохой оценкой, если распределение "с тяжёлыми хвостами" или иными отклонениями от нормальности.