Доказательство, что π равно 17 – 8√3

[semigradsky]

Доказательство индийского математика.

Где ошибка в "доказательстве"?

[Booker48]

semigradsky
Полагаю, вам самому лениво разбирать 22 страницы заведомой лажи?

[Red_Herring]

semigradsky в сообщении #1705142 писал(а):

Доказательство индийского математика.

Заведомая ошибка называть этого альтернативного гения математиком и тащить эту глупость сюда.

[lel0lel]

semigradsky в сообщении #1705142 писал(а):

Где ошибка

В шестом знаке после запятой.

[Mihr]

lel0lel в сообщении #1705155 писал(а):

В шестом знаке после запятой.

Разве не в третьем?

[Red_Herring]

Mihr в сообщении #1705160 писал(а):

Разве не в третьем?

а какая разница? хоть в 1000000ом

[Mihr]

Red_Herring в сообщении #1705161 писал(а):

а какая разница? хоть в 1000000ом

Принципиальной разницы, конечно, нет. Но если в 1000000ом, то ощущение фокуса всё-таки ярче

[lel0lel]

Точно, даже в третьем. Это я невнимательно посмотрел, в ожидании "фокуса")

[Ed_Em]

А в военное время по приказу прапора число π может быть равно четырем! ©
☺

[ozheredov]

Booker48
Кстати, если эти 22 страницы заведомой лажи разделить на 7 страниц заведомой лажи - получим лучшее приближение к $\pi$

[miflin]

ozheredov в сообщении #1705172 писал(а):

если эти 22 страницы заведомой лажи разделить на 7

Только-только собрался написать именно это, но тут удар ниже пояса от ozheredov.

[Null]

semigradsky в сообщении #1705142 писал(а):

Где ошибка в "доказательстве"?

Автор доказательства использует ни где не объясненную трансформацию, которая изменят площади.

[Евгений Машеров]

ozheredov в сообщении #1705172 писал(а):

Кстати, если эти 22 страницы заведомой лажи разделить на 7 страниц заведомой лажи - получим лучшее приближение к $\pi$

Увы, не получим. Там 23 страницы...

Вообще же - подобные "доказательства" всерьёз должны интересовать специалистов вне данного Форума, а именно психиатров. Как "сверхценная идея". Для математика это может быть более или менее остроумным софизмом, который интересно разобрать и найти ошибку. Но копаться в достаточно объёмном тексте утомительно. Насколько можно понять при беглом рассмотрении - автор исходит из числа $\pi$ в формуле площади круга, круг он приближает двенадцатиугольником, а площади сегментов, отсекаемых сторонами двенадцатиугольника, приравнивает к площади неких треугольников. Что может быть приближённо верно, но никогда не будет верно в точности, даже возьми он 144-, 1728- или 20736-угольник.
Подобное приближение было бы достижением для античности (величина 3.1436 куда точнее вавилонского 3.125 или египетского 3.16, но хуже приближения Архимеда 3.14286 или приближения Птолемея 3.1417, причём оба они предлагали не как точное значение, а как удобное для расчётов, сознавая его приближённость). И даже в древней Индии Ариабхата и Бхаскара пользовались более точным 3.1416.

[Dendr]

Глянул и ужаснулся. Хотя можно все не читать, "ключевая идея" - на предпоследней странице, где приводится утверждение, что суммарная площадь 4 прямоугольных треугольников равна суммарной площади 8 криволинейных треугольников. Все остальное - попытки доказать его (?).

Mihr в сообщении #1705160 писал(а):

Разве не в третьем?

Вообще я человек ленивый, и в геометрических кунштюках разбираюсь плохо. Поэтому набросал программку на "плюсах" найти представление для "пи" получше, но в том же виде - $a-b\sqrt{c}\approx\pm\pi$
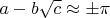
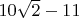
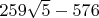
Выглядящее хрестоматийным $10\sqrt{2}-11$, которое в 4-м знаке сбивается, что уже лучше статейного, можно даже и не упоминать. Есть и дальше (ну это очевидно) примеры. Вот это тоже, может, подогнать под что-то получится: $259\sqrt{5}-576$ оно дает ошибку в пятом знаке.
Перебирая "руками" $b$ и $c$, понятное дело, можно найти и еще ближе.

Вот этот монстр - лучшее, что нашлось, дальше не имело смысла, разрядов плавающей точки все равно не хватает: $5004839-50840\sqrt{9691}$.
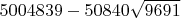
Аж 13 знаков правильных - перепроверил в Вольфраме.