Правильно ли подсчитал?

[Altenter]

Здравствуйте. Требуется проверить правильно ли совершен подсчет количества вершин разного типа.
Есть куб, со стороной $c$, сложенный из единичных кубиков.
Есть фигура, которая получается путем вырезания из куба со стороной $c$ куба со стороной $a$ вместе с одной из вершин куба $c^3$.
Места расположения вершин маленьких кубиков будем называть вершинами.
В получившейся фигуре есть:
1). 10 вершин, инцидентных одному единичному кубику.
2). 3 вершины, инцидентных 3-м единичным кубикам.
3). 1 вершина, инцидентная 7-ми единичным кубикам.
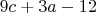
4). $9c+3a-12$ вершин, которые инцидентны 2-м единичным кубикам.
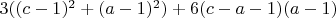
5). $3((c-1)^2+(a-1)^2)+6(c-a-1)(a-1)$ вершин инцидентных 4-м кубикам.
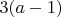
6). $3(a-1)$ вершин инцидентных 6-ти кубикам
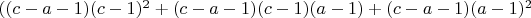
7). $((c-a-1)(c-1)^2+(c-a-1)(c-1)(a-1)+(c-a-1)(a-1)^2$ вершин, инцидентных 8-ми кубикам.

Для куба со стороной $b$ есть:
1) 8 вершин, инцидентных 1 кубику.
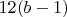
4) $12(b-1)$ вершин, инцидентных 2-м кубикам.
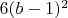
5) $6(b-1)^2$ вершин, инцидентных 4-м кубикам.
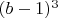
7) $(b-1)^3$ вершин, инцидентных 8-ми кубикам.
И в нем нет вершин 2),3),6).
Правильно ли это?

Вершины 2-7 разлагаются на вершины низших порядков также как разлагаются целые числа на целые слагаемые.