Как решать двумерные СЛАУ с зависимыми коэффициентами?

[Ed_Em]

Сразу объясню, что за задача. Итак, имеем альт-азимутальный телескоп (БТА). Для избавления от различных механических проблем в его системе управления используется классический набор коэффициентов СКН (системы коррекции наведения) из восьми коэффициентов. Под спойлером в конце - собственно подробности.
Так вот, часть этих коэффициентов (K3 и K4) фигурирует в поправках как к азимуту (dA), так и зенитному расстоянию (dZ).
Сейчас я считаю следующим образом. Сначала вычисляю нуль-пункты (K0 и K5), затем наименьшими квадратами вычисляю K3-K7 (без K5, который уже посчитал, и набор данных на него скорректировал) для dZ, затем вычисляю поправку к dA на нуль-пункт и K3/K4, после чего остается найти K2 и K3.
Такое решение в корне некорректно, кроме того, дает сильные осцилляции и на двух наборах данных, полученных в одну и ту же ночь, может выдавать достаточно сильно различающиеся коэффициенты (при этом остаточные невязки вполне сносные).

Вот, собственно, и вопрос: а как решать правильно такие системы уравнений? Т.е. по сути имеем двумерную функцию от двух аргументов (на прочие не обращайте внимания, т.к. они взаимосвязаны с A/Z) и восьми параметров. По нескольким десяткам измеренных неточностей наведения у меня есть таблица значений этой функции.
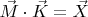
Если решать классически вида $\vec{M}\cdot\vec{K}=\vec{X}$, где в вертикальный вектор X собрать и dA, и dZ, то K3/K4 получатся разными.
Если же сначала наименьшими квадратами получить K1-K3 и K6-K7, а потом полученное решить совместно, суммируя остаточные dA/dZ, получим еще хуже…

// здесь нет, оказывается, тега [spoiler], поэтому так:

Формулы:

$$dA = K_0 + K_1\cdot\tg Z + K_2\frac{1}{\sin Z} - K_3\frac{\sin A}{\tg Z} + K_4\cdot\cos\delta\frac{\cos P}{\sin Z}$$

$$dZ = K_5 + K_6\cdot\sin Z + K_7\cdot\cos Z + K_3\cdot\cos A + K_4\cdot\cos\varphi\cdot\sin A$$

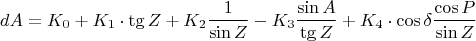
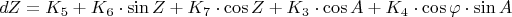
Здесь:

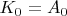• $K_0 = A_0$ - нуль-пункт азимута;
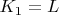• $K_1 = L$ - наклон горизонтальной оси;
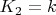• $K_2 = k$ - коллимационная ошибка;
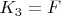• $K_3 = F$ - широтная ошибка вертикальной оси;
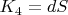• $K_4 = dS$ - ошибка времени (сейчас она почти нулевая, так что, теоретически хоть от этого коэффициента можно избавиться; однако, практически получаем ненулевую величину);
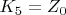• $K_5 = Z_0$ - нуль-пункт зенитной оси;
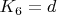• $K_6 = d$ - гнутие трубы (синусоидальный компонент);
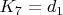• $K_7 = d_1$ - гнутие трубы (косинусоидальный компонент).

Как пример, вот один из наборов коэффициентов:

#    K0      K1      K2      K3      K4      K5      K6      K7
  -88.00   +8.00  +39.70   -3.00   +2.70 -108.50  +22.80  +30.00

Как видите, здесь еще и налицо даже в одном наборе линейная зависимость от одинаковых тригонометрических функций…
В будущем хотим перейти на сплайны или ортонормированные полиномы на полусфере с "дыркой" (хоть те же Цернике можно попробовать), но пока что есть, то есть...

[Евгений Машеров]

А можно подробнее о задаче? Нужно оценить набор коэффициентов $K_i$, зная дельты от А и Z для разных углов? Тогда мне напрашивается банальный регрессионный анализ. Возможно, ридж-регрессия на случай мультиколлинеарности.
Или иное нужно?

[Ed_Em]

Да мне уже объяснили, что можно для начала попробовать тупыми наименьшими квадратами, собрав общую матрицу: прямоугольную - по всем коэффициентам (где их нет - пишем нули), "надставив" друг над другом матрицы выражений для dA и dZ. Аналогично, "надставив" сами $dA_i$ и $dZ_i$, получаем правую матрицу-столбец.
Еще не проверял, недели через две вернусь из отпуска и попробую.

Просто напрягает то, что выражения имеют явные линейные зависимости в коэффициентах: таки когда придумывались СКН, никто не думал, что будут решать обратную задачу. Считалось, что коэффициенты можно измерить механически и получить результат...

[Евгений Машеров]

Вот ридж-регрессия могла бы и помочь.
$\hat{a}=(X^TX+\alpha I)^{-1}X^Ty$
Добавляя маленькую альфу, избавляем инвертируемую матрицу от необратимости (которая при точной линейной зависимости регрессоров; при приближённой обратить можно, только вот результат формально есть, но дисперсия оценок неприлично растёт, а при небольшом изменении данных они "прыгают")
Выбор коэффициента, увы, неформализован (хотя можно, скажем, скользящим экзаменом)

[Евгений Машеров]

Если я правильно понял постановку - надо оценить коэффициенты $K_{1..7}$, зная измеренные при разных A, Z, P, $\varphi, \delta$ величины ошибок $dA, dZ$ - то я бы воспользовался регрессией, до того намеряв бы отсчётов при значениях углов таких, чтобы регрессоры были бы как можно более ортогональны. Если они окажутся строго линейно зависимы - вообще оценок не получится, а чем больше ортогональности - тем точнее оценки. А так как этого, вполне возможно, удастся добиться только в очень малой степени - то использовать ридж-регрессию.
Вектор $y$ (зависимая переменная) будет состоять из значений ошибок $dA, dZ$, а матрица регрессоров $X$ будет (для обычной процедуры, где свободный член оценивается до обращения матрицы) включать вспомогательную переменную, для $dA$ равную нулю, а для $dZ$ единице (тогда $K_0$ будет равен свободному члену, а $K_5$ сумме свободного члена и коэффициента при этой переменной). Для $K_1$ регрессор равен $\tg Z$ для игреков, соответствующих $dA$ и нулю для соответствующих $dZ$, аналогично для $K_2$ будет $\frac 1 {\sin Z}$ и ноль. Для $K_{6,7}$ аналогично, но нулевые для $dA$ и по соответствующей формуле для $dZ$. Для $K_{3,4}$ выбирается нужная формула для регрессоров.
Далее $\hat{K}=(X^TX+\alpha I)^{-1}X^Ty$ (при нулевой альфе это обычная регрессия, но если регрессоры коррелированы, а есть основания это подозревать, дисперсия коэффициентов неприлично растёт, и зависимость от малых изменений игреков, как и от добавления/исключения наблюдений увеличивается). Можно провести расчёт для серии значений, и посмотреть, как коэффициенты меняются (они, вообще говоря, уменьшаются и уменьшается их разброс).

[Ed_Em]

Евгений Машеров, спасибо. Почитаю подробней про этот метод.