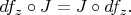Антилинейное - значит антиголоморфное?

[OlgaD]

У меня возник вопрос о связи двух свойств комплексного отображения. Пусть у нас есть комплексное векторное пространство $V,$ на котором определено антилинейное отображение $\theta:V\to V$ (точнее вещественная структура, т.е. дополнительно $\theta^2=id_V$). Есть предположение, что это отображение будет также антиголоморфным. Но я не уверена, что могу это показать. Есть ли такая связь?

[dgwuqtj]

А что вы называете антиголоморфным отображением? Если $V \cong \mathbb C^n$ конечномерно, то я бы предположил, что это такое $\theta \colon \mathbb C^n \to \mathbb C^n$, что все его координаты $\theta_i \colon \mathbb C^n \to \mathbb C$ после композиции с комплексным сопряжением становятся голоморфными (как функции многих переменных). Просто про конечномерность вы не написали.

[OlgaD]

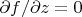
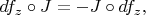
Под антиголоморфным отображением я и понимаю отображение, сопряженное к которому является голоморфным. Конечномерность предполагается. Только я не уверена, что смогу посчитать у такого отображения производную. Кажется, помимо равенства $\partial f/\partial z=0$ есть еще условие антиголоморфности отображения в матричной форме. Что-то вроде $df_z\circ J=-J\circ df_z,$ где $J$ - комплексная структура. Т.е. функция $f$ называется антиголоморфной, если ее производная является антилинейной в каждой точке. Но пока все вычисления провести не могу.
А условие голоморфности отображения - это коммутирование с комплексной структурой, т.е. $df_z\circ J=J\circ df_z.$

[dgwuqtj]

Тогда будем считать, что $V = \mathbb C^n \cong \mathbb R^{2 n}$, а $\theta$ задано вещественной матрицей $2 n \times 2 n$. Можете найти его (вещественный) дифференциал? И выразить антилинейность в терминах компонент $\theta$?

[OlgaD]

Это навряд ли. Я могу только предположить, что если у нас есть комплексные координаты $z=(z_1,\ldots,z_n),$ то в этих координатах мы можем записать $\theta(z)=A\bar z,$ где $A$ некоторая матрица. Дифференцировать выражения, содержащие матрицу, я не умею. Поэтому как отсюда получить $d\theta_z\circ J=-J\circ\theta_z$ я не знаю.