Векторные сферические гармоники

[yesterday]

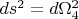
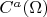
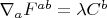
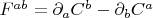
Пусть задана метрика $ds^2=d\Omega^2_4$. Единичная сфера $S^4$. На ней задан вектор $C^a(\Omega )$. Интересуют собственные числа решения $\nabla_a F^{ab}=\lambda C^b$, где $F^{ab}=\partial_aC^b-\partial_b C^a$. В общем, собственные числа решения уравнения Максвелла на единичной сфере для векторных гармоник. Это же, наверно, известная вещь. Не могу толком найти.

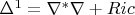
Собственные попытки решения--Bochner's formula $\Delta^1=\nabla^*\nabla+Ric$ и статья Alan Chodos and Eric Myers, annals of physics, 1984. Harmonics on the N-sphere.

Но, я думаю, вещи то известные уже, просто я туплю.