Классификация&преобразование элементов квадрата из квадратов

[Altenter]

Здравствуйте.
Проблема первая:
Пусть имеем квадрат со стороной $a>2$, сложенный из единичных квадратов, количество которых очевидно $a^2$.
Проведем классификацию единичных вершин ребер и граней этого квадрата и определим их количество:
Вершины квадрата:
$ V_1=4; V_2=4(a-1); V_4=(n-1)^2. $

Вершины возможные при удалении или добавлении квадратиков к квадрату:
$V_3$.

Ребра квадрата, соединяющие соответствующие вершины:
$ R_{12}=8; R_{22}=4(a-2); R_{24}=4(a-1); R_{44}=(a-1)(a-2) $.

$R_{11}$ - ребро единичного отдельного квадрата.
Это ребра возможные при преобразованиях квадрата:
$ R_{13}; R_{23}; R_{33}; R_{34} $.

Невозможное единичное ребро:
$R_{14}$.

Грань единичного квадрата:
$G_{1111}$

Грани квадрата:
$ G_{1224}=4; G_{2244}=4(a-2); G_{4444}=(a-2)^2 $.

Теперь осталось классифицировать грани, которые принципиально невозможны и грани, которые возможны при преобразованиях квадрата, т.е. возникают при присоединении к нему дополнительных квадратиков или вырезании из него этих квадратиков вместе с их ребрами и вершинами, но все это представить в голове не очень получается, всего возможно $4^4=256$ вариантов индексации граней, задача в том, чтобы выделить из них возможные, а затем среди этих возможных выделить те, которые идентичны и переходят друг в друга поворотами на $\frac{\pi}{2}$, т.е. определить все неэквивалентные грани. А также аналогично все возможные в результате преобразований квадрата и все невозможные грани.

И вот это первая проблема.
Ну можно исключить сразу 9 возможных видов граней квадрата из 256 и 1 единичную, остается 246. И вот как вот все это вращать в голове, строить из квадратов фигуры, соответствующие каждому набору индексов и выяснять, что возможно, а что нет?

Проблема вторая:
Очевидно вершины, ребра и грани единичных квадратов при присоединении единичных квадратов к квадрату могут преобразовываться соответственно в вершины, ребра и грани другого типа. Некоторые из которых могут также складываться и преобразовываться друг в друга. Образуют ли эти преобразования группу или другую алгебраическую структуру? И как ее построить???

Грубо говоря у нас есть бесчисленное множество единичных квадратов, мы можем их складывать грань к грани, ребро к ребру. Т.е. укладывать в единичную квадратную решетку и вырывать обратно и получать единичные кубики и какие-то виды элементов в фигуре. Количество видов этих преобразований конечно, как и количество видов элементов. Как его построить?
Предполагаю, что узлы пустой квадратной решетки надо пронумеровать как вершины с индексами 0: $V_0$, пустые ребра как $R_{00}$, а пустые грани $G_{0000}$ и затем вкладывать туда единичные квадратики и складывать индексы, чтобы получались возможные.

[mihaild]

Ничего непонятно. Какая "классификация", какие "преобразования"?

[Altenter]

mihaild в сообщении #1704681 писал(а):

Ничего непонятно. Какая "классификация", какие "преобразования"?

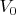
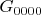
Есть бесконечная плоская единичная квадратная решетка узлы которой проиндексированы как $ V_0$, ребра как $R_{00}$, грани как $G_{0000}$. Также отдельно есть счетное множество единичных квадратов вершины которых имеют индекс $V_1$, ребра $R_{11}$, Грани $G_{1111}$.
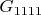
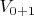
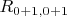
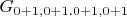
Укладываем в решетку связно единичные квадраты. Вот уложили один единичный квадрат в решетку, теперь индексы ячейки с квадратом в этой решетке стали: у четырех вершин $V_{0+1}$, у четырех ребер $R_{0+1,0+1}$, у грани $G_{0+1,0+1.0+1,0+1}$, далее в соседнюю ячейку уложили второй квадрат. У них появилась общая сторона в ячейке, но в эту сторону каждый квадрат вложил по ребру, т.е. ребро стало двойным, а в каждый конец этого ребра каждый из квадратов вложил по вершине, т.е. 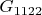в каждом из этих двух узлов решетки по 2 вершины квадратов, соответственно индексы этих узлов станут $V_2$, а индекс ребра между ними $R_{22}$, индексы граней тоже измеятся и станут $G_{1122}$(с точностью до поворота), Теперь в перпендикулярном длинной стороне полученного прямоугольника добавим еще единичный квадрат. 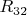В один из узлов решетки при этом лягут 3 вершины и индекс этого узла станет $V_3$, 2 ребра, соединяющие этот узел с соседними приобретут индекс $R_{32}$, а два других $R_{31}$.

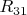
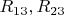
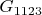
Если мы имеем заполненный квадрат на этой решетке, то выше описано какие элементы с какими индексами в нем могут быть. Но если мы из этого квадрата извлекаем квадратики или добавляем, то появляются нехарактерные для квадрата элементы, как например вершины $V_3$ и ребра $R_{13},R_{23}$, а также нехарактерные для квадрата грани $G_{1123}$ например.

Количество всех индексов для граней $4^4=256$, но грань далеко не со всяким индексом реализуется физически. А те, которые реализуются, могут быть эквивалентны с точностью до поворота. Необходимо выбрать те виды граней из 256, которые реализуются, а затем выделить из них неэквивалентные. Аналогично и с ребрами. Затем среди реализующихся неэквивалентных выбрать те, которые входят в структуру квадрата. Это первая проблема.

Далее, как было показано выше, элементы преобразуются друг в друга, например при попадании в один узел решетки с индексом $V_0$ 3-х вершин $V_1$, этот узел преваращается в $V_3$, преобразования ребер, вершин и граней происходят связно, т.к. мы добавляем в решетку квадратики, а не отдельно вершины или ребра. Количество вариантов конечно. Составляют ли эти варианты преобразования элементов алгебраическую структуру? - это вопрос 2.

-- 06.10.2025, 19:09 --

Интересно вот что, всего возможных индексов ребер 16:

11,12,13,14
21,22,23,24
31,32,33,34
41,42,43,44

Так вот, 11- единичное ребро.
14 и 41 - это невозможные ребра.
Принадлежащие квадрату ребра: 12,21,22,24,42,44,
Не принадлежащие квадрату: 13,31,23,32,33,34,43.

Ребра 12 и 21 - эквивалентны с точностью до поворота. 24 и 42 также эквивалентны.
Итого
неэквивалентных ребер, принадлежащих квадрату: 12,22,24,44
неэквивалентных не принадлежащих квадрату: 13,23,33,34
Поровну, по 4.
Плюс одно единичное ребро.
Итого неэквивалентных ребер 9.
Теперь надо проделать то же самое для граней- это первая проблема.

Цифры получились сплошь красивые 4+4=8, 4+4+1=9, 7+6=13, 7+6+1=14, 8+8=16, 8+8+2=18.

[mihaild]

Всё еще не очень понятно.
Вот у нас есть решетка. Если я правильно понимаю, то каждой грани приписано, заполнена эта грань илит нет. И по заполненности граней как-то вычисляются "индексы" вершин, ребер, граней.
Вроде бы "индекс" вершины - число инцидентных ей заполненных граней, "индекс" ребра - неупорядоченная пара индексов инцидентных ему вершин, "индекс" грани - кортеж индексов инцидентных грани вершин с точностью до сдвига (а зеркальное отражение разрешено, или обход всегда в одну сторону?).
Так?

[Altenter]

mihaild в сообщении #1704694 писал(а):

(а зеркальное отражение разрешено, или обход всегда в одну сторону?).

Зеркало пока нет.

mihaild в сообщении #1704694 писал(а):

Так?

Все верно.