Эффективные оценки и неравенство Рао-Крамера

[meshok]

Доброго времени суток!
Пытаюсь разобраться в следующих утверждениях.
Пусть у нас дана вероятностно-статистическая модель, которая удовлетворяет условиям регулярности. Тогда для каждой несмещенной оценки $\hat{\theta}$ параметра $\tau(\theta)$ справедливо неравенство Рао-Крамера, причем равенство достигается тогда и только тогда, когда семейство является экспоненциальным и

$$\hat{\theta}(X_1,\ldots,X_n)-\tau(\theta)=\frac{\tau'(\theta)u_\theta(X_1,\ldots,X_n)}{n I_{X_1}(\theta)}.$$

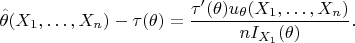
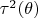
Эта часть утверждения понятна. Но есть следующий факт, что эффективная оценка сущесвует (т.е. в неравенстве Р-К достигается знак равенства) только для какой-то одной функции $\tau$ (с точностью до линейных преобразваний), т.е. если есть эффективная оценка для $\tau(\theta)$, то для $\tau^2(\theta)$ уже найти эффективную оценку нельзя. Везде, где я видел, про этот факт говорится, что его легко видеть из равенства, приведенного выше. Единственное, что приходит в голову, это решить линейный однородный диффур относительно $\tau$ и уже как-то посредством этого показывать единственность, но это вроде бы не подходит под фразу "легко видеть.."
Может кто-нибудь подсказать, как здесь нужно рассуждать?

[ShMaxG]

Пусть $T_1(X)$ является эффективной оценкой для $\tau_1(\theta)$, а $T_2(X)$ является эффективной для $\tau_2(\theta)$. Рассмотрите ковариационную матрицу вектора $(T_1(X),T_2(X))$. Она вырождена, а значит $T_1(X)$ и $T_2(X)$ линейно связаны. Далее от этой связи рассмотреть матожидание.

[meshok]

Спасибо!