Как доказать, что такой функции нет

[Divergence]

В прикладной задаче нужно найти функцию
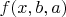
$f(x,b,a)$, где $x>0$, $0 < b \le c\le 1$,
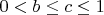
которая непрерывно дифференцируема по $x,a,b$ во всех точках области определения.

Для функции должны выполняться условия

$$ f(x,b,1)=x^{b-1}$$

$$ f(x,b,b)=x^{b-1}$$

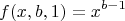
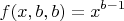
для всех $x>0$ и $0<b\le1$.
Первое условие выполняется, например, для функций

$$ f(x,b,a)=x^{b-a}$$

$$ f(x,b,a)=x^{b/a-1}$$

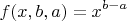
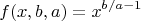
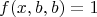
Но второе условие не выполняется, так как $$ f(x,b,b)=1$ для этих примеров.

Как можно найти функцию, удовлетворяющую сразу двум условиям или доказать, что таких функций нет?
Заранее спасибо.

[svv]

$f(x,b,a)=x^{b-1}$ независимо от $a$?

[Divergence]

Нужна функция трех переменных и должна активно зависеть от $a$.
Видимо, чтобы исключить "независимость от а", мне нужно третье условие записаное как второе $f(x,a,a)=x^{a-1}$?

[svv]

Divergence в сообщении #1703857 писал(а):

должна активно зависеть от $a$

Тогда $x^{b-1 + (a-b)(1-a)}$

[Divergence]

Спасибо.
Я не догадался это квадратное выражения запихнуть в показатель, а пытался рассмотреть как множитель.:)

[svv]

Как множитель можно, только надо прибавить $1$:
$x^{b-1}\bigl(1+(a-b)(1-a)\bigr)$
Ещё:
$x^{b-1}+(a-b)(1-a)$

[Divergence]

Спасибо, но такие функции не подходят по физическому смыслу задачи. Степенная то, что нужно.

-- 30.09.2025, 11:26 --

Исходно интересовала комбинация двух функций $g(x,a)= x^{a-1}$ и $g(x,b)=x^{b-1}$
такая, что $f(x,a,b):=F(g(x,a),g(x,b))$ удовлетворяла указанным условиям.

[svv]

В терминах $F(u,v)$ получаем условия:
$F(v,v)=F(1,v)=v$

[Divergence]

Мне нравиться больше ваш предыдущий ответ

$$ f(x,b,a) = g(x,a) \, \Bigl(\frac{g(x,a)}{g(x,b)}\Bigr)^a$$

или

$$ f(x,b,a) = g(x,b) \, \Bigl(g(x,a)\Bigr)^{(b-a)}$$