Минимальное число камней для разбиений

[gipokrat]

У Насти есть несколько красивых камушков (не обязательно равных по весу). Для каждого натурального $n$, не превышающего 5, Настя может распределить эти камушки на две группы так, что камушки в одной группе будут в $n$ раз тяжелее, чем в другой. Какое наименьшее число красивых камушков может быть у Насти?

[lel0lel]

Можно полную массу камней положить равной любому числу. Выберем $120$, тогда годятся такие массы $30,30,26,14,10,10$ -- всего шесть камней. Чтобы показать, что пяти камней не хватит можно записать предполагаемую линейную систему шести уравнений с пятью неизвестными массами. Должны реализовываться кучки камней с массами $(120,60,40,30,20,24)^T$ -- это столбец свободных коэффициентов. Система будет несовместной, так как ранг расширенной матрицы системы будет всегда больше ранга матрицы системы (которая состоит из единиц и нулей).

[gipokrat]

lel0lel
У меня 5 камней получилось: 2, 3, 10, 15, 30.
Осталось лишь доказать, что 4 не хватит.

[lel0lel]

gipokrat
Ошибся я, спасибо. Систему не рассматривал внимательно, просто выдал желаемое за действительное.

[lel0lel]

gipokrat в сообщении #1703670 писал(а):

Осталось лишь доказать, что 4 не хватит.

Пусть ненулевые массы камней $m_1, m_2, m_3, m_4$ и $\sum m_i=60$. Из условия задачи должны существовать кучки с массами $30,20,15,12,10.$
Случай 1. Пусть $m_1=30, m_2+m_3+m_4=30.$ В этом случае есть $6$ кучек с массами меньше $30$. Их массы: $m_2,30-m_2,m_3,30-m_3,m_2+m_3,30-m_2-m_3.$ Из этих $6$ кучек должны быть четыре с массами $20,15,12,10.$ Видно, что это возможно только если все массы камней -- целые числа. Также видно, что должен присутствовать камень с нечётной массой, поскольку одна из кучек имеет массу $15$. В таком случае, среди масс $m_2,30-m_2,m_3,30-m_3,m_2+m_3,30-m_2-m_3$ есть четыре нечётные массы, поэтому значения масс $20,15,12,10$ получить нельзя.
Случай 2. Пусть $m_1+m_2=30, m_3+m_4=30.$ Не ограничивая общности, положим $m_1\geq m_2, m_3\geq m_4$ и $m_1\geq m_3$, тогда $m_1\geq m_3\geq 30-m_3\geq 30-m_1.$ И в этом случае есть $6$ кучек с массами меньше $30$. Их массы: $m_1,30-m_1,m_3,30-m_3,60-m_1-m_3,30-m_1+m_3.$ Из этих $6$ кучек должны быть четыре с массами $20,15,12,10.$ Снова массы камней должны быть целыми и должен присутствовать камень с нечётной массой. В таком случае, среди масс $m_1,30-m_1,m_3,30-m_3,60-m_1-m_3,30-m_1+m_3$ четыре будут нечётные, поэтому значения $20,15,12,10$ получить нельзя.
Это доказывает, что четырёх камней для выполнения условия задачи недостаточно.

[Dendr]

Если не только до пяти? Попробовал обобщить и набросал "на коленках" программку (то есть без попыток оптимизировать), которая тупо перебирает все возможные разбиения числа $N$ (НОК чисел от единицы до $n+1$) на $k$ слагаемых так, чтобы выполнялись требования из условия.

Соответственно, основная задача - найти минимальное количество слагаемых, для которых это возможно, дополнительная - подсчитать количество способов разбиения.

Получилось так:
До 2 - 3 камня, единственный способ (понятно и так, это 1-2-3)

До 3 - 4 камня, 4 способа (приведу все: 1 2 3 6, 1 2 4 5, 1 3 3 5, 2 3 3 4)

До 4 - 5 камней, 55 способов

До 5 - 5 камней, 29 способов

До 6 - 6 камней, 739 способов
Например: 45, 60, 70, 80, 84, 101.

До 7 - 7 камней, подсчёт количества способов упирается в вычислительные способности компьютера, найдено лишь несколько.
Самый симпатичный, и его можно было даже найти "вручную": 90, 105, 105, 112, 120, 140, 168

Дальше уже совсем не потянул.

[lel0lel]

Dendr в сообщении #1704196 писал(а):

Например: 45, 60, 70, 80, 84, 101.

Полная сумма должна быть кратна $3$ и $7$. Наверное, закралась опечатка.

Dendr в сообщении #1704196 писал(а):

До 7 - 7 камней, подсчёт количества способов упирается в вычислительные способности компьютера, найдено лишь несколько.
Самый симпатичный, и его можно было даже найти "вручную": 90, 105, 105, 112, 120, 140, 168

Запишем это так

$$S=2\left(\frac{S}{8}\right)+\frac{S}{7}+\frac{S}{6}+\frac{S}{5}+\frac{2S}{15}+\frac{3S}{28}.$$

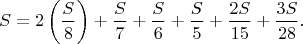
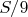
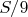
Из этого легко получить восемь камней с делимостью из условия до $8$ и так далее. Разобьём один камень с массой больше $S/9$ так, что появится $S/9$ и остаток. Например $S/6=S/9+S/18$:

$$S=\frac{S}{9}+2\left(\frac{S}{8}\right)+\frac{S}{7}+\frac{S}{5}+\frac{2S}{15}+\frac{3S}{28}+\frac{S}{18}.$$

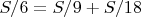
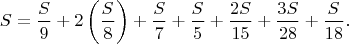
Вообще, так с самого начала и надо было действовать:

$$S=\frac{S}{2}+\frac{S}{2}=\frac{S}{2}+\frac{S}{3}+\frac{S}{6}=\frac{S}{3}+\frac{S}{4}+\frac{S}{4}+\frac{S}{6}=\frac{2S}{15}+\frac{S}{5}+\frac{S}{4}+\frac{S}{4}+\frac{S}{6}$$

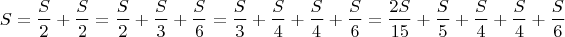
И вот этот-то (не единственный) вариант, благодаря, уже имеющейся дроби $\frac{S}{6}$ подходит и при делимости до натурального $5$. Дальше можно продолжить колоть камни:

$$\frac{2S}{15}+\frac{S}{5}+\left(\frac{S}{7}+\frac{3S}{28}\right)+\frac{S}{4}+\frac{S}{6}=2\left(\frac{S}{8}\right)+\frac{S}{7}+\frac{S}{6}+\frac{S}{5}+\frac{2S}{15}+\frac{3S}{28}.$$

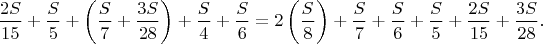
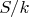
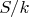
В общем, если в каком-то случае удастся расколоть камень так, что остаток будет $S/k$, где $k$ - целое, до которого делимость из задачи ещё не дошла, то когда дойдёт до построения минимального набора камней к этой делимости, камни колоть нужды нет, так как камень $S/k$ уже в наличии. Примерно так и произошло при делимости до $5$, камень $S/6$ уже образовался ранее. Возможно ли, что такая ситуация будет повторяться дальше -- надо думать.

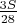
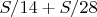
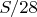
Похоже, что да, может. Когда будем выполнять требование делимости до $13$, возьмём из общей груды камень с массой $\frac{3S}{28}$. Колем его так: $S/14+S/28$. Таким образом, когда надо будет выполнять делимость до $27$ нужный камень $S/28$ в куче уже есть.

[Dendr]

lel0lel в сообщении #1704208 писал(а):

Наверное, закралась опечатка.

Точно.
Взгляд соскочил, когда перепечатывал строку. Вот так правильно: 45 60 70 80 81 84.
Хотя лучше, наверное, привести семейство вариантов, которые можно отыскать "вручную". Базовый - 10 21 35 60 84 210
Альтернативы:
4 21 35 66 84 210
21 25 35 45 84 210
21 31 35 39 84 210

Тут просто - зная, что успех будет, легко "придумать" логику. Нам нужно набрать суммы 210, 140, 105, 84, 70 и 60. Так что назначим камни 210 (тяжелее нельзя) и 84 (самый "кривой"). Ко второму будем добавлять, чтобы набрать следующие суммы - то есть камни 21 и 35. Нам еще нужно два камня общей массой 70 (еще одна сумма уже получилась), так что осталось взять камень массы 60. Или камень, дополняющий уже имеющиеся (21, 35 и их комбинацию 56).