С. А. Теляковский в Сборнике задач по теории функций действительного переменного, Наука, 1980 писал(а):
3.31. Определить неотрицательную аддитивную, но не

-аддитивную функцию на алгебре всех подмножеств рациональных чисел из
![$[0,1]$. $[0,1]$.](https://dxdy-03.korotkov.co.uk/f/6/b/1/6b16d9f4fd0b4b361b5c3c0462414bd582.png)
Не понимаю, чем эта задача отличается от задачи найти неотрицательную аддитивную, но не сигма-аддитивную функцию на алгебре всех подмножеств

. А я знаю только одно решение -- с ультрафильтрами (описано под оффтопом)
(Оффтоп)
"возьмём" какой-нибудь неглавный ультрафильтр

на множестве

и для любого множества

положим
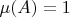
, если
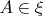
, и

, если
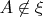
. Тода из свойств ультрафильтра следует, что
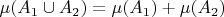
для непересекающихся

,

. При этом
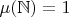
, а
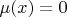
для любого

, так как ультрафильтр

не главный.
Что, интересно, автор имел ввиду? Может тут дело в том, что он допускает значения

?