Оценка условного события, зная пересечения двух

[seraphimt]

Здравствуйте, подскажите, пожалуйста, по задаче.
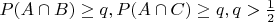
$P(A\cap B) \geq q, P(A\cap C) \geq q, q > \frac{1}{2}$. Нужно доказать, что $P(A|B\cap C) \geq q$
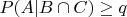
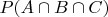
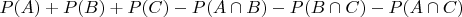
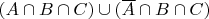
Очень нужен какой-то намёк, куда вообще нужно думать, ибо потратил уже часы и часы и всё впустую. Пробовал раскрывать $P(A\cap B \cap C)$ через $P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C)- P(A \cap C)$, $B \cap C$ представлял как $(A\cap B \cap C) \cup (\overline{A} \cap B \cap C)$ и тд, получаются только тривиальные оценки в духе больше $-q$ или меньше двух =_=.

[mihaild]

Обозначим $P(A \cap (B \setminus C)) = x$, $P(A \cap (B \setminus C)) = y$, $P(B \cap C) = z$, $P(A \cap B \cap C) = t$.
Из условий, $x + y + z \leq 1$ (1) (как сумма вероятностей несовместных событий), $x + t \geq q$, $y + t \geq q$. Надо доказать что $t \geq zq$.
Предположим противное, $t < zq$ или $z > t / q$.
Из (1), $z \leq 1 - x - y$, что дает $t / q < 1 - x - y$ или $t < q - qx - qy$.
С другой стороны, $t \geq q - \frac{x + y}{2}$.
Отсюда уже несложно получить противоречие.