Тестировал кое-что по работе связанное с ИИ (ChatGPT 5, платный по API без никаких ограничений) и черт меня дернул завести "разговор" о квантовой информации.
Если что ничего про ней не знаю, только краем уха слышал что она "должна сохраняться" (в изолированной системе разумеется).
Далее переразказ "разговора".
Итак речь везде конкретно идет про частиц фермионов спина 1/2 (электрон).
Сначала обсуждалась ситуация если частица/ы в чистом состоянии:
По Шеннону, информация в битах получаемая при измерении спина в некотором направлении
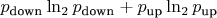
, где

это соответные вероятности получить up или down.
Интегрируя по всем направлениям в сфере блоха (всевозможными направлениями спина в чистом состоянии), получаем среднюю информацию о состоянии спина при измерении ~0.721 бит (для частицы в чистом состоянии).
Я проверил выкладки, смысл вычислений и интеграл - и результат математически верный (потвердил в wolfram alpha).
Интересно тут то, что для эта средняя информация та же самая независимо от того, известно ли наперед или нет чистое состояние (т.е. в каком направлении ориентирован спин). Разница в том что если чистое состояние известно то мы выбирая ось измерения мы можем по желанию варьировать получаемую информацию при однократном измерении с нуля до 1 бит (поперек); но средняя информация (при измерении в случайном направлении) одна и та же 0.721 бит.
Очевидно, число 0.721 бит имеет место только если измеряемая частица в чистом состоянии.
Если например она полностью запутана с второй - то частица "сама по себе" окажется с полностью смешанной матрице плотности, вероятность up или down по любой оси одна и та же 1/2 и соотвено получаемая информация о состоянии при измерении по всех осей равна 1, соответно то же самое для среднем - 1 бит.
Бот сказал что число 0.721 бит хорошо известный рассчет для случая частицы полуцелого спина в чистом состоянии.
Тогда я предложил рассмотреть изолированную систему из измерителя спина (он также запоминает измеренные спины) и каком-то количестве частиц. Для верности пусть считаем что все они находятся в пространственно замкнутом плоском 3d торе (чтоб вопросов про изолированности не возникало). Можно считать что прибор типа кувыркается и иногда сталкиваясь с частицами, измеряет (и запоминает) их спины.
Пусть частицы сначала в полностью смешанном состоянии. При первых случайных измерений прибор "получит" инфу 1 бит (тем самым ставя частицу в чистое состояние). При дальнейших измерений он продолжит получать в среднем 0.721 бит при каждом измерении.
Т.е. как бы в замкнутой системе со времени информация должна возрастать неограниченно что вроде противоречит "квантовом сохранением информации".
Бот объяснил это типа при каждом измерении якобы "возникающая информация" компенсируется с тем что у измерителя огромнейшее количество микроскопических степеней внутренней свободы (при увеличения неопределенности которых, он все еще может "оставаться прибором").
Тем не менее, если все это продолжится достаточно долго - то в итоге прибор теряя внутренюю информацию должен начать "деградировать" до степени неспособности измерять/запоминать спины (т.к. он должен терять из своих определенности состояния внутренних степеней свободы 0.721 бит при каждом измерении, чтобы скомпенсировать лишнюю инфу) - т.е. в предельном случае состояние "прибора" должно стать настолько неопределенным, что будет непонятно это прибор или камень или что-то другае с той же энергии покоя.
Бот как ни странно, подтвердил - что в достаточно долгом пределе (порядка количества микроскопических степеней внутренних свободы прибора, при которых он все еще остается прибором) измерений спина так и будет - да, прибор должен "деградировать".
Он "объяснил" это тем что прибор неограниченно запутываясь с измеряемыми частицами, в итоге окажется в настолько запутанном состоянии, что ничего вычленить и измерить не получится.
Ладно. Все это мне показалось довольно странным.
В основном мне не нравилось как исчисляется информация. Частица ведь принципиально случайна.
Я предложил другой рассчет.
Все что можно знать о частице, исчерпывается знанием ее матрице плотности.
Если мы знаем матрицу плотности частицы - то мы знаем все что о ней вообще можно знать. Т.е. если мы ее знаем наперед, то что бы мы там не меряли - мы никакой больше информации о матрице плотности (прежде измерения) не получим в результате измерения - так как мы ее совершенно точно ее наперед знали и без того.
В частности, пусть например мы знаем что частица в полностью смешанном состоянии (в любом направлении измерить спин вверх будет 1/2) - результат измерения не даст никакую новую информацию про то что мы и так знали.
Т.е. в этой парадигме, "полученная информация" из измерения исчисляется по байесовской формуле изменения ожиданий про матрицу плотности, вследствие результата измерения.
После некоторого обсуждения про ограничений и соответных степеней свободы матрице плотности, бот вывел вроде бы правдоподобную формулу как по байесу рассчитать инфу получаемую о матрице плотности в результате одиночного измерения. (разумеется речь идет про получения информации о матрице плотности прежде измерения, после него она всегда известна т.к. измерение ставит частицу в известном чистом состоянии).
В такой парадигме "получаемой информации" получилось 2.19 бит на измерение. Я выкладки не проверял (рассчет сделал вслепую в волфраме, по формулу предложенную ботом) но тут возник такой вопрос/парадокс (который от верности данного вычисления не зависит).
Если инфу при измерении считаем по-байесу как уменьшение неизвестности о матрице плотности - при рассмотрении физического случая выше (прибор измерения спина измеряет случайно спины в изолированой системе), физически итог в пределе получается качественно другим.
Изначально частицы пусть в неизвестном состоянии матрице плотности - прибор измерит каждую из них однократно (получая 2.19 бит - или сколько там верно - информации, т.е. уменьшая неизвестность о том какова была матрица плотности на 2.19 бит) - и дальнейшие измерения над уже измеренными частицами, никакую новую инфу не вытащат (т.к. они уже в известном чистом состоянии).
Выходит - прибор НЕ "деградирует" а останется вполне хорошим измеряющим прибором, сколько бы он не кувыркался и не измерял те же самые частицы в замкнутом 3d.
Конечно, в обоих случаев - разное определение "получаемой информации" (она о разном) - тем не менее, физический результат (останется ли прибор прибором, или деградирует до степени неузнаваемости) - не может зависеть от нашего выбора как и какую информацию считать.
Когда я указал на это, бот начал бубнить что на самом деле прибор не деградирует и второй метод "вернее" (не смотря на то, что он прежде говорил наоборот, и что 0.721 бит на измерение встречается в литературе - а другой подход про "знание" или "незнание" матрицы плотности якобы нет или реже обсуждался).
В чем предмет обсуждeния:
- "деградирует" или "не деградирует" прибор измерения спина на самом деле в рассмотреной выше ситуации (изолированно взаимодействуя с конечном количестве частиц, на неограниченно длинный период)
- Имеют ли вообще подходы выше "по Шеннону" чего-то общего с "квантовой информации", или все это чушь собачья
На всякий случай: мне совершенно ясно что LLMs это просто генераторы правдоподобного продолжения текста. Просто было проще чтобы она писала выкладки и обоснования, а я их проверял (в мере своих способностей :).
Мой анализ: возможно сам вопрос ill-posed. Он про изолированную систему из "классического измерителя спина" и квантов. Но "квантовая информация сохраняется" только при чисто-квантовой системе с унитарной эволюции. Возможно классический измеритель спита "все портит" - ведь в классике никакого "сохранения информации" нет. С другой стороны, это вроде говорит что квантовомеханическое рассмотрение в пределе больших систем никак нельзя свести к классике (в изолированных систем).