Задачка по ТФКП

[gris]

Понадобилось извлечь корень третьей степени из комплексного числа. А всё забыл. Помогите, люди добрые. Вспоминаю ТФКП
$\sqrt[3]{-46-9i}=?$
Показательная форма $z=-46-9i=\sqrt{46^2+9^2}\cdot e^{i\cdot\arctg(9/46)}$
$\sqrt[3]{z}=z^{1/3}=\sqrt[3]{\sqrt{46^2+9^2}}\cdot e^{i\arctg{3/46}}=\sqrt{13}...$
А что дальше? Или как вообще эти штуки решаются?

А вот ещё: преобразовать
$\dfrac {1+\cos a +i\sin a}{1+\cos a - i \sin a}; a \in (0,\pi /2)$
Домножаю на сопряжённое к знаменателю (т.е. числитель)
$=\dfrac {(1+\cos a +i\sin a)^2}{(1+\cos a)^2 -(i \sin a)^2}$
$=\dfrac {1+\cos^2 a -\sin^2 a+2\cos a+2i\sin a +i\sin 2a}{(1+\cos a)^2 +\sin^2 a}$

[dgwuqtj]

Вам его надо численно посчитать, что ли? Все кубические корни — это $\omega^k (2 - 3 i)$, где $\omega = \frac {-1 + i \sqrt 3} 2$ и $k \in \{ 0, 1, 2 \}$.

[lel0lel]

gris Фаза на пи больше. И тройка как-то у вас хитро под арктангенс заскочила. Корней будет три, но не так красиво как у dgwuqtj, либо с синусом и косинусом арктангенса придётся возиться.

[gris]

lel0lel
Ой, с тройкой оплошал. Арктангенс не линейный. Да как это решать просто? Я в Вольфрам залез, но хотят решение с объяснением... Короче, вечером открою <для себя> Шабата

[lel0lel]

gris в сообщении #1701485 писал(а):

Да как это решать просто?

Не знаю как просто, ответ dgwuqtj, конечно, намекает, что нужно извлечь корень кубический из единицы (он многозначный), а затем найти хоть один корень из всего числа. Наверное можно неопределенными коэффициентами его найти.

[nnosipov]

gris в сообщении #1701485 писал(а):

Короче, вечером открою <для себя> Шабата

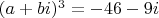
Берите сразу 2-й том... Да какая ТФКП, это обычная алгебра. В данном случае общая формула для извлечения корня (та, что с тригонометрией) заведет в тупик. Здесь предполагалось, что корень будет извлекаться тупо по определению: пишем $(a+bi)^3=-46-9i$ с вещественными неизвестными $a$, $b$ и затем решаем систему. Правда, в процессе решения системы возникнет кубическое уравнение, которое --- внимание! --- ни в коем случае не следует решать по формуле Кардано (иначе процесс пойдет по кругу). А нужно всего лишь тупо угадать рациональный корень этого уравнения (если угодно, найти его по известному алгоритму через делители свободного и старшего коэффициентов).

[Утундрий]

Это если есть подозрение, что задача учебная, то есть, составлена тупым возведением в куб чего-нибудь простенького. А иначе только через модуль и фазу, выражающуюся через аркфункции.

[nnosipov]

Утундрий в сообщении #1701496 писал(а):

Это если есть подозрение

Естественно. Здесь оно есть. Команда в Maple

evala((-46-9*I)^(1/3));

сразу его материализует, и остается только сделать видимость "честного решения".

[gris]

Да проблема дурацкая. Некий студент спросил совет, как решить задачи так, чтобы понравилось преподу. Я не знаю, какие там требования, а спрашивать у ИИ или Вольфрама они и сами умеют. Насчёт второго не уверен В общем — тупик. Но меня напугало то, что я принялся делать и затормозил. Так и забуду, как решать квадратные уравнения И как тогда жыть?

[lel0lel]

gris в сообщении #1701478 писал(а):

вот ещё: преобразовать
$\dfrac {1+\cos a +i\sin a}{1+\cos a - i \sin a}; a \in (0,\pi /2)$

Напрашиваются комплексные экспоненты, потом в числители и знаменателе вынести за скобки такие экспоненты, чтобы в скобках остались почти синус и почти косинус.

[Утундрий]

gris в сообщении #1701499 писал(а):

забуду, как решать квадратные уравнения И как тогда жыть?

Достаточно помнить саму идею дополнения до квадрата.

[provincialka]

Во второй задаче можно ещё к половинному углу привести.

[Padawan]

lel0lel в сообщении #1701506 писал(а):

Напрашиваются комплексные экспоненты, потом в числители и знаменателе вынести за скобки такие экспоненты, чтобы в скобках остались почти синус и почти косинус.

Там одно и то же остается и сокращается, соответственно. Получается в итоге $e^{ia}$.

[wrest]

gris в сообщении #1701499 писал(а):

Некий студент спросил совет, как решить задачи так, чтобы понравилось преподу.

Построить решения на комплексной плоскости циркулем и линейкой?