Фактическое "покрытие" рац. чисел отрезками

[artempalkin]

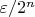
Возьмем все рациональные числа на отрезке $[0,1]$ и пронумеруем. Далее, накроем их в соответствии с их номерами отрезками длины $\varepsilon/2^{n}$. Суммарная длина такого покрытия не может быть больше $\varepsilon$, что означает, что мера рациональных чисел равна нулю.

Теперь вопрос! Можно ли придумать такое фактическое покрытие рациональных чисел отрезками с $\varepsilon=1/2$ (например... или с любым другим, но конкретным), чтобы мы имели фактическое иррациональное число, которое отрезками не покрыто?

[mihaild]

Что такое "фактическое покрытие", "фактическое число"?
Возьмите ваше любимое иррациональное число $x$, и при построении покрытия, если очередной интервал накрывает $x$, сокращайте его, продолжая накрывать нужную точку, пока $x$ не окажется вне него.

[Null]

Ну покрываем рациональные числа так, чтобы $\sqrt{2}$ в них не попадало. Длинные отрезки кидаем далеко от этой точки.

[artempalkin]

mihaild в сообщении #1701018 писал(а):

Что такое "фактическое покрытие", "фактическое число"?

Означает конкретное отображение, если хотите $\mathbb{Q}\cap[0,1]\to\{[a,b]|0\leqslant a < b \leqslant 1\}$, при этом сумма длин отрезков конечна и меньше $1$. Например, так.

mihaild в сообщении #1701018 писал(а):

Возьмите ваше любимое иррациональное число $x$, и при построении покрытия, если очередной интервал накрывает $x$, сокращайте его, продолжая накрывать нужную точку, пока $x$ не окажется вне него.

Это понятно, но и вы понимаете, чтО я имею в виду. Вы лично видели такие покрытия?

Null в сообщении #1701019 писал(а):

чтобы $\sqrt{2}$ в них не попадало

Оно и не попадет, но я вас понял :)

[mihaild]

artempalkin в сообщении #1701022 писал(а):

Вы лично видели такие покрытия?

Я лично и просто множества всех рациональных чисел не видел :)
Поправить итеративный алгоритм так, чтобы он на каждом шаге давал множество меры ровно $1/2 - 1/2^n$, не включающее $1/\sqrt{2}$, несложно. И явно выписать границы каждого интервала. Написать какую-то формулу из простых операций - не уверен (формулой даже явную нумерацию рациональных чисел записать не слишком просто, хотя и можно), но и не очень понятно, зачем.

[artempalkin]

mihaild в сообщении #1701024 писал(а):

Поправить итеративный алгоритм так, чтобы он на каждом шаге давал множество меры ровно $1/2 - 1/2^n$, не включающее $1/\sqrt{2}$, несложно. И явно выписать границы каждого интервала.

типа, if $1/\sqrt2\in[a,b]$ do... вот так поправить? Скучновато, хотя и понятно...

mihaild в сообщении #1701024 писал(а):

но и не очень понятно, зачем

Тот же вопрос можно задать относительно вообще изучения мной математики :) И, думаю, многими форумчанами.

[Mikhail_K]

artempalkin в сообщении #1701022 писал(а):

Вы лично видели такие покрытия?

Ну, ничего диковинного нет в покрытии множества $\mathbb{Q}\cap[0,1]$ отрезками, не покрывающим какое-то конкретное иррациональное число.

Например, рассмотрим отрезки $\left[0,\,\frac{\sqrt 2}{2}-\frac{1}{n}\right]$, $n=2,3,4,\ldots$ и $\left[\frac{\sqrt 2}{2}+\frac{1}{n},\,1\right]$, $n=4,5,6,\ldots$. Эти отрезки покрывают все рациональные числа из $[0,1]$, но не покрывают число $\sqrt{2}/2$. Пусть это покрытие и построено не так, как Ваше.

[artempalkin]

Mikhail_K в сообщении #1701029 писал(а):

Например, рассмотрим отрезки $\left[0,\,\frac{\sqrt 2}{2}-\frac{1}{n}\right]$, $n=2,3,4,\ldots$ и $\left[\frac{\sqrt 2}{2}+\frac{1}{n},\,1\right]$, $n=4,5,6,\ldots$. Эти отрезки покрывают все рациональные числа из $[0,1]$, но не покрывают число $\sqrt{2}/2$. Пусть это покрытие и построено не так, как Ваше.

Чёт я не вижу, как сумма длин этих отрезков стремится к нулю

[Mikhail_K]

artempalkin в сообщении #1701073 писал(а):

Чёт я не вижу, как сумма длин этих отрезков стремится к нулю

Ну да, у моих отрезков сумма длин не будет сколь угодно малой. Я просто не очень понял вопрос: он сформулирован так, как будто покрытие всех рациональных чисел и непокрытие при этом конкретного иррационального - это что-то странное и необычное. Что, мол, теоретически оно может и существует, а пример и не привести. Своим примером я продемонстрировал, что нет, дело вполне обычное.

[RIP]

Честно говоря, вопрос не очень понятен. Например, покроем число $a/b\in[0,1]\cap\mathbb{Q}$ отрезком $\left[\frac{a}{b}-\frac{1}{10b^2},\frac{a}{b}+\frac{1}{10b^2}\right]\cap[0,1]$. При этом число $\sqrt{1/2}$ останется непокрытым. Такое устроит?

Или так. Покроем число $a/b\in[0,1]\cap\mathbb{Q}$ отрезком $\left[\frac{a}{b}-\frac{\varepsilon}{b^{2.1}},\frac{a}{b}+\frac{\varepsilon}{b^{2.1}}\right]\cap[0,1]$. При достаточно малом $\varepsilon>0$ число $\sqrt[3]{1/2}$ останется непокрытым, но никто не знает пример конкретного такого $\varepsilon$ (то есть понятно, что $\varepsilon=10^{-100}$ годится, но доказывать это никто не умеет).

[Geen]

artempalkin в сообщении #1701016 писал(а):

Можно ли придумать такое фактическое покрытие рациональных чисел отрезками с $\varepsilon=1/2$ (например... или с любым другим, но конкретным), чтобы мы имели фактическое иррациональное число, которое отрезками не покрыто?

Например, с $\varepsilon=1$... нельзя