Я имею отношение к квантовой и структурной химии, и слышал как люди, занимающиеся газовой электронографией, употребляли фразу “квантовики решают прямую задачу, а мы увы обратную”. Эта фраза мне понятна: расчёт изначально находит структуру и другие свойста, а в электронографии структура определяется через МНК (градиентный спуск) по экспериментальным данным. Хотя и в квантовой химии задачи “не до конца прямые”.
В действительности же, по-моему, любые задачи в математике в той или иной степени обратные, и вообще вся математика посвящена решению обратных задач. Возьмём для примера пять уравнений:





Чтобы решить первую задачу, нужно провести одно деление. Вторая задача решается через детерминант. Третья задача решается по формуле Кардано, чётвёртая, если не ошибаюсь, решается очень похожим образом через резольвенты, а пятая в общем случае “не решается”, точнее её нельзя решить аналитически.
По сути, все пять задач – это обратные задачи от простого уравнения n-й степени. Т.е. если мы пишем, например,
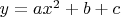
, то нахождение y по известному x – это прямая задача, а нахождение x по известному y – это обратная задача.
Признаки прямой задачи:
1) Её можно решить в любом интервале x;
2) Для любого x решение единственно;
3) Решение относительно простое по сравнению с обратной задачей;
4) Сложность (время) и надёжность решения прямой задачи практически не зависит от того, чему равен x или какое было начальное приближение;
5) Ещё одна связь между прямой и обратной задачей: существуют очень простые и универсальные методы решения обратной задачи через прямую, в частности простой перебор или градиентный спуск.
Теперь я предлагаю такую идею: взять пять уравнений выше и определить для них сложность решения обратной задачи. Сложность решения задачи можно измерить количественно – количеством машинного времени, потраченного на её решение с применением наилучшего алгоритма.
У меня сильное подозрение, что для первых четырёх задач сложность будет описываться некой простой зависимостью от номера (например, экспонентой), а для пятой сложность будет выпадать из этой зависимости. И из этого можно будет заключить, что в математике есть нерешённая задача – найти “сверхформулу Кардано”, которая позволит решить пятое уравнение аналитически.
Сложность прямой задачи для этих четырёх уравнений тоже растёт, хотя не очень сильно. И возникает ещё один вопрос: как сложность обратной задачи в общем случае зависит от сложности прямой. Я предполагаю что эта зависимость, может быть, экспоненциальная, или скажем экспонента от экспоненты (это как-то называется?).
У меня ещё вопрос такой: какие бывают принципиальные виды подходов, позволяющие решать обратную задачу, если известно как решать прямую? Я вижу три таких подхода – простой перебор, градиентный спуск, и ещё может быть итерационное решение по теории возмущений. Что ещё знаете?