Дивергенция от декартовых к цилиндрическим координатам

[Divergence]

Пытаюсь получить из уравнения дивергенции в декартовых координатах

$$ (D1) \qquad \operatorname{div} {\bf F} \, = \, \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} , $$

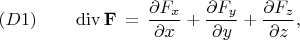
уравнение дивергенции в цилиндрических координатах

$$ (D2) \qquad \operatorname{div} {\bf F} \, = \, \frac{\partial F_r}{\partial r} + \frac{1}{r} \frac{\partial F_{\phi}}{\partial \phi} + \frac{\partial F_z}{\partial z} . $$

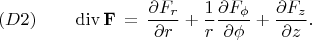
Получаю в формуле (D2) лишне слагаемое $+F_r/r$.


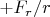
Использую для этого две формулы

$$ (1a) \qquad \frac{\partial}{\partial x} = \frac{\partial r}{\partial x} \frac{\partial}{\partial r} + \frac{\partial \phi}{\partial x} \frac{\partial}{\partial \phi} + \frac{\partial z}{\partial x} \frac{\partial}{\partial z} = \cos \phi \, \frac{\partial}{\partial r} \, - \, \frac{\sin \phi}{r} \frac{\partial}{\partial \phi} $$

$$ (1b) \qquad \frac{\partial}{\partial y} = \frac{\partial r}{\partial y} \frac{\partial}{\partial r} + \frac{\partial \phi}{\partial y} \frac{\partial}{\partial \phi} + \frac{\partial z}{\partial y} \frac{\partial}{\partial z} = \sin \phi \, \frac{\partial}{\partial r} \, + \, \frac{\cos \phi}{r} \frac{\partial}{\partial \phi} $$

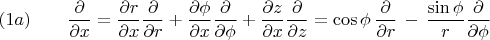
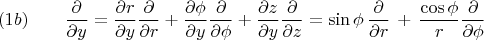
и формулы

$$ (2a) \qquad F_x = F_r \cos \phi - F_{\phi} \sin \phi , $$

$$ (2b) \qquad F_y = F_r \sin \phi + F_{\phi} \cos \phi , $$

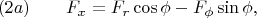
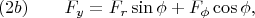
которые получил из формул

$$ (3a) \qquad e_r = e_x \cos \phi + e_y \sin \phi , $$

$$ (3b) \qquad e_{\phi} = - e_x \sin \phi + e_y \cos \phi , $$

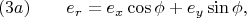
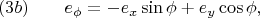
из условия

$$ (F) \qquad {\bf F} = F_x e_x + F_y e_y + F_z e_z = F_r e_r + F_{\phi} e_{\phi} + F_z e_z . $$

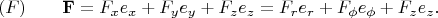
Подставляя формулы (1a), (1b), и (2a), (2b) в уравнение (D1) получаю

$$ (D3) \qquad \operatorname{div} {\bf F} \, = \, \frac{\partial F_r}{\partial r} + \frac{1}{r} \frac{\partial F_{\phi}}{\partial \phi} + \frac{\partial F_z}{\partial z} + \frac{1}{r} F_r . $$

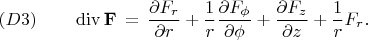
Использование формул (1a), (1b), и (3a), (3b) позволило мне получить уравнение градиента в цилиндрических координатах.
Поэтому подозреваю ошибку в формулах (2a), (2b).

И где же у меня ошибка?
Заранее спасибо.

[Divergence]

Извиняюсь. Все получается. Неправильно написал формулу дивергенции (D1). Должно быть так

$$ (D1new) \qquad \operatorname{div} {\bf F} \, = \, \frac{1}{r} \frac{\partial (r F_r)}{\partial r} + \frac{1}{r} \frac{\partial F_{\phi}}{\partial \phi} + \frac{\partial F_z}{\partial z} . $$

Ошибок нет.