На какую наибольшую степень числа 3 может делиться сумма?

[waxtep]

Даёшь бесконечнцатку (бесконечку?)!

Я попробовал на эту тему немного арифметики, правда, далеко не ушёл. Мы знаем (теорема Вильсона), что $\forall p\in\mathbb{P}:p|1+(p-1)!$. Если посмотреть в целом на сумму пар $b_s=s!+(p-s)!\pmod{p}$, то легко получить рекурренцию (далее все равенства по модулю $p$):

$$b_s+s\cdot b_{s+1}=s!(s^2+s+1)$$

Эта рекурренция даже решается явно:

$$b_s=s!+\frac{(-1)^s}{(s-1)!}$$

Выглядит симпатично, правда, как дальше действовать, - непонятно. Для щлемоблещущих чисел (простых $p=2t+1$, на которые делится бесконечное количество факториальных сумм) должно быть

$$\sum_{s=1}^{t}b_s=0$$

а заодно получается забавное тождество для любого простого $p=2t+1$:

$$\sum_{s=1}^{t}(s+t)!-\frac{(-1)^s}{(s-1)!}=0$$

-- 14.09.2025, 02:45 --

...которое, конечно, следует из полученного почленно

$$(p-s)!(s-1)!\equiv{(-1)^s\pmod p}$$

[Dmitriy40]

Усложним задачу: будем искать сумму не факторилаов, а примориалов, 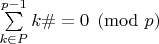$\sum\limits_{k \in P}^{p-1} k\# = 0 \pmod p$. И полную, и почленно.
Для полной нашёл лишь два решения: 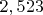$2,523$.
Для почленной лишь максимум четвёрка:

(Оффтоп)

Показывается лишь максимальная найденная длина, более короткие игнорируются если не дают полную нулевую сумму:

2: [], len=0, FOUND
19: [5], len=1
31: [7], len=1
61: [53], len=1
67: [41], len=1
103: [41], len=1
107: [53], len=1
109: [89], len=1
127: [89], len=1
139: [89], len=1
149: [37], len=1
199: [71], len=1
241: [97], len=1
251: [197], len=1
283: [263], len=1
349: [73], len=1
383: [151], len=1
421: [173], len=1
463: [59], len=1
509: [347], len=1
523: [521], len=1, FOUND
577: [443], len=1
599: [23, 547], len=2
727: [191, 643], len=2
1667: [1049, 1091], len=2
2039: [827, 1171], len=2
4421: [1801, 2591], len=2
6247: [827, 5303], len=2
6779: [5197, 5237], len=2
7193: [167, 2833], len=2
8017: [6469, 7621], len=2
8147: [13, 5003], len=2
8699: [457, 8369], len=2
9931: [673, 1381], len=2
11239: [3391, 10141], len=2
14221: [809, 11717], len=2
16619: [4157, 12101], len=2
16963: [2287, 9277], len=2
17383: [4637, 4969], len=2
21563: [11399, 19777], len=2
22273: [9787, 14323], len=2
22283: [2843, 17539], len=2
23599: [19471, 23327], len=2
24229: [6857, 15307], len=2
25943: [6131, 7507], len=2
26903: [4799, 18233], len=2
28163: [15991, 18493], len=2
29837: [14753, 15923], len=2
30071: [6343, 8863], len=2
32939: [12007, 15313], len=2
33487: [3527, 25889], len=2
37897: [3253, 24781], len=2
41131: [23017, 34381], len=2
41539: [10313, 22691], len=2
44263: [19427, 42407], len=2
46271: [9907, 32687], len=2
49957: [31477, 36833], len=2
51263: [9199, 44563], len=2
55903: [137, 52543], len=2
58099: [727, 8861], len=2
59387: [7681, 40507], len=2
59419: [16139, 29131], len=2
65633: [4679, 47657], len=2
67631: [31957, 55439], len=2
69263: [2531, 47237], len=2
69833: [22453, 35281], len=2
71711: [17827, 58771], len=2
72103: [1039, 52579], len=2
73609: [20063, 33049], len=2
74383: [61, 20399], len=2
74933: [26953, 73819], len=2
78839: [3191, 75937], len=2
79817: [4789, 23789], len=2
81901: [10151, 63793], len=2
81937: [30869, 60527], len=2
87911: [11471, 11833], len=2
88667: [10039, 84221], len=2
88741: [7933, 13693], len=2
89317: [39829, 67763], len=2
92189: [1117, 7937], len=2
98627: [6469, 35339], len=2
98713: [9601, 41771], len=2
98873: [23159, 38047], len=2
99137: [61403, 75709], len=2
99907: [31531, 95273], len=2
109387: [77587, 87211], len=2
119419: [8663, 95549], len=2
123289: [37811, 64381], len=2
132739: [14759, 113797], len=2
134371: [30577, 124427], len=2
137519: [93053, 131311], len=2
141221: [33247, 41057], len=2
147163: [55609, 111791], len=2
151813: [66523, 105613], len=2
156727: [28597, 31019], len=2
160087: [42013, 120413], len=2
161459: [41149, 102871], len=2
161923: [37861, 74779], len=2
163781: [41203, 81637, 135353], len=3
284447: [4943, 6337, 274301], len=3
491039: [23873, 58613, 66293], len=3
551723: [5077, 160373, 200909], len=3
695801: [374321, 437093, 467237], len=3
735283: [241919, 340643, 536509], len=3
939061: [172313, 377347, 931267], len=3
947743: [269561, 442517, 935699], len=3
1050977: [200983, 1008419, 1046791], len=3
1301173: [607493, 672587, 708137], len=3
1301561: [284591, 573523, 1033271], len=3
1342573: [472163, 1142041, 1248001], len=3
1561801: [369487, 963841, 1431809], len=3
1912879: [398821, 994817, 1021091], len=3
2035399: [230977, 1374619, 1968341], len=3
2455337: [497989, 629059, 1503829], len=3
2800283: [673513, 2153491, 2291659], len=3
2845303: [888211, 1228567, 1582799], len=3
3238597: [988693, 1199663, 2661557], len=3
3280357: [612113, 1217299, 2466839], len=3
3305779: [589349, 2357573, 3196559], len=3
3327409: [894073, 2783353, 3273287], len=3
3356173: [522439, 2526169, 2755219], len=3
3396829: [2270689, 2780993, 2992321], len=3
3517253: [141131, 1625977, 1979689], len=3
3555007: [1814083, 2394299, 3427141], len=3
4672009: [689917, 1430201, 1747121], len=3
4756181: [19597, 1167317, 3150817], len=3
4780037: [2785099, 3349543, 3568217], len=3
6653659: [325463, 1428473, 5353031], len=3
6709331: [297169, 4841581, 6109277], len=3
6727949: [867067, 2868343, 4532743], len=3
6816151: [949853, 1541117, 2101259], len=3
6873641: [280249, 3153629, 6618041], len=3
6877043: [117917, 1573079, 2162401], len=3
7078073: [3268373, 3372983, 4949033], len=3
7366217: [3709319, 3957773, 4508939], len=3
7615073: [3199991, 4317023, 4645721], len=3
8052043: [653311, 1294303, 6507727], len=3
8269559: [420799, 6481259, 7760059], len=3
9142321: [1827593, 6184687, 8489191], len=3
9178649: [6114763, 6223817, 6338957], len=3
9475831: [353321, 4295671, 6616667], len=3
9692477: [3458219, 3845537, 6350107], len=3
9906991: [195997, 5064023, 5449931, 5909749], len=4

(Программа на PARI)

rez=vector(100); minlen=1;
forprime(p=0,1e7,
   fn=Mod(1,p); sn=Mod(0,p); n=0;
   forprime(k=2,p-1, fn*=k; sn+=fn; sn==0&&rez[n++]=k; );
   if(n>=minlen || sn==0,
      print(p,": ",rez[1..n],", len=",n,if(sn==0,", FOUND",""));
      minlen=n;
   );
);

[Dmitriy40]

Оказывается исходный вопрос проверили ещё шесть лет назад до $2^{40}$ и решений не найдено (кроме $3$ и $11$). Две статьи в архиве, одна 2014г с $144\times10^6$ до $2^{34}$, вторая 2019г дальше до $2^{40}$.

[waxtep]

Dmitriy40, спасибо, интересно! Я так понял они пытаются найти контрпример к гипотезе Курепы (та же сумма, но начиная с $0!$, на единичку больше), но посматривают и по сторонам (сумма с единицы, сумма степеней факториалов).
А чтобы вероятность найти контрпример сравнялась с классической вероятностью встретить динозавра, расчёт надо теперь тянуть до $2^{80}$

[Dmitriy40]

А ещё сразу публикуют самые близкие к нулю ($|r_p|<100$) найденные результаты, что и позволяет утверждать что нужной суммы ($r_p=1$) нет начиная с 144млн (а ниже проверил mihaild) и до $2^{40}$.