Упростить выражение

[Утундрий]

Вот любопытно, а как без кубических уравнений доказать, что

$$3\cdot \left( 2+\dfrac {10}{\sqrt {27}} \right)^{1/3}+2\cdot \left( 2+\dfrac {10}{\sqrt {27}} \right)^{-1/3}=6$$

[worm2]

Можно с квадратным: $3x+2/x=6$. Решаем, получаем $x=1\pm\sqrt{1/3}$. Потом возводим в куб. Все преобразования обратимы.

[Утундрий]

И правда.

А если мы не знаем, что это шестёрка?

[wrest]

Достаточно показать, что одно слагаемое равно $3-\sqrt{3}$, а другое равно $3+\sqrt{3}$ - проверяется прямым возведением в куб.

[wrest]

Ну а найти это можно, используя тот факт что числа вида $p+q\sqrt{3}$ (с рациональными $p,q$) образуют замкнутое множество относительно умножения и возведения в степень.

Тогда, несложными эквивалентными арифметическими преобразованиями приведя слагаемые к виду $\sqrt[3]{54\pm30\sqrt{3}}$ будем упрощать до вида $54\pm30\sqrt{3}=(p+q\sqrt{3})^3$ методом неопределенных коэффициентов, и так найдём что $\sqrt[3]{54\pm30\sqrt{3}}=3\pm\sqrt{3}$
Это конечно в каком-то виде всё равно решение кубического уравнения, но вроде несложно, и не требуется заранее знать что сумма равна 6.

[nnosipov]

Утундрий в сообщении #1700595 писал(а):

А если мы не знаем, что это шестёрка?

Если априори известно, что правая часть является рациональным числом, то это число должно быть целым (поскольку слагаемые в левой части суть целые алгебраические числа). Теперь приближенно вычисляем левую часть и получаем результат вблизи $6$. Значит, справа может быть только $6$.

-- Чт сен 04, 2025 00:10:05 --

wrest в сообщении #1700611 писал(а):

Это конечно в каком-то виде всё равно решение кубического уравнения

Можно обойтись без решения кубических уравнений. Искомые числа $p$ и $q$ должны быть целыми или дробными (но с заранее известными знаменателями), поэтому их можно найти, вычисляя приближенно числа $\sqrt[3]{54+30\sqrt{3}} \pm \sqrt[3]{54-30\sqrt{3}}$.

[maxal]

Стандартные вычисления с алгебраическими числами: https://sagecell.sagemath.org/?q=uzglru

[dmd]

Через результант

[nnosipov]

dmd
То есть, на неизвестное значение левой части составляется уравнение, которое затем все-таки нужно решить, чтобы найти $x=6$. А ТС хочет вообще без уравнений обойтись.

-- Чт сен 04, 2025 09:46:56 --

maxal в сообщении #1700626 писал(а):

Стандартные вычисления с алгебраическими числами

А как они там реализованы? Небось, тоже какие-то уравнения решаются.

[dmd]

nnosipov
Думаю, не верным будет говорить, что это подобно решению уравнения. Внутри результанта матричные операции и модульная арифметика. Тоже самое можно получить делением полиномов с остатком, но за большее количество шагов.

[nnosipov]

dmd
Да не в результанте дело. На последнем этапе Вы используете факторизацию, т.е. фактически решаете уравнение (результант же не возникает сразу в разложенном виде).

[dmd]

nnosipov
Тогда да, согласен. Надо посмотреть, какие алгоритмы используются в CAS при полиномной факторизации.

[maxal]

nnosipov в сообщении #1700637 писал(а):

А как они там реализованы? Небось, тоже какие-то уравнения решаются.

Как я понимаю, алгебраические числа представляются минимальными многочленами и интервалами для изоляции конкретного корня. Никакие уравнения не решаются (если только явно не попросить),но производятся действия над многочленами - например, вычисление результантов и их факторизация. Для установления, что какое-то алгебраическое число это 6, нужно лишь показать, что его минимальный многочлен равен $x-6$.

[nnosipov]

maxal в сообщении #1700781 писал(а):

алгебраические числа представляются минимальными многочленами и интервалами для изоляции конкретного корня

Ок. Тогда то, что я выше предложил, как раз в этом ключе.

Вот подробное изложение. Пусть $u,\,v \in \mathbb{Q}$, $u \neq 0$, $v>0$, $\sqrt{v} \not\in \mathbb{Q}$. Мы хотим выяснить, является ли число

$$r=\sqrt[3]{u+\sqrt{v}}+\sqrt[3]{u-\sqrt{v}}$$

рациональным, и если да, то записать $r$ как рациональное число, не решая никаких уравнений. Домножая $r$ на подходящее целое число (например, на общий знаменатель $u$ и $v$), мы можем считать числа $u$ и $v$ целыми. Тогда $\alpha=\sqrt[3]{u+\sqrt{v}}$ и $\beta=\sqrt[3]{u-\sqrt{v}}$ суть целые алгебраические числа. Если $r \in \mathbb{Q}$, то должны найтись такие $a,\,b \in \mathbb{Q}$, что

$$u+\sqrt{v}=(a+b\sqrt{v})^3.\eqno(*)$$

Имеем

$$ a+b\sqrt{v}=\alpha, \quad a-b\sqrt{v}=\beta,$$

откуда находим

$$2a=\alpha+\beta, \quad 2vb=(\alpha-\beta)\sqrt{v}.$$

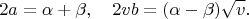
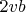
Следовательно, числа $2a$ и $2vb$ должны быть целыми. При этом единственную пару-кандидат $(a,b)$ можно указать явно:

$$a=\frac{[\alpha+\beta]}{2}, \quad b=\frac{[(\alpha-\beta)\sqrt{v}]}{2v}$$

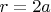
(здесь $[x]$ --- целая часть числа $x$). Проверить эту пару $(a,b)$ можно подстановкой в $(*)$. Если она проходит проверку, то находим $r=2a$, если не проходит --- число $r$ иррационально.

[maxal]

nnosipov в сообщении #1700786 писал(а):

Тогда то, что я выше предложил, как раз в этом ключе.

Не совсем, т.к. вы используете свойства чисел конкретного вида. Чисто алгоритмическое решение такое: научится вычислять минимальные многочлены степеней, включая корни (это просто), сумм и произведений алгебраических чисел, заданных минимальными многочленами (ну и интервалом для корня). А это делается через результанты. Конкретный вид чисел (например, в виде иррациональностей) здесь не важен, все работает автоматически.

В вашем примере мы стартуем с минимальных многочленов $x-u$ для $u$ и $x^2-v$ для $\sqrt{v}$ и пошагово строим минимальный многочлен для всего выражения $\sqrt[3]{u+\sqrt{v}}+\sqrt[3]{u-\sqrt{v}}$. Если получившийся многочлен имеет степень 1, то выражение рационально, иначе - нет.