Запишем решение уравнения
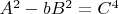
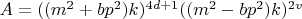
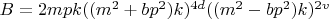
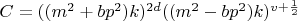 -- 02.09.2025, 11:22 --
-- 02.09.2025, 11:22 --Проверим решение уравнения:
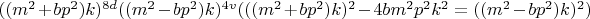 -- 02.09.2025, 11:27 --
-- 02.09.2025, 11:27 --Найдем решение уравнения
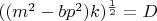
в целых числах при
 -- 02.09.2025, 11:32 --
-- 02.09.2025, 11:32 --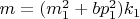
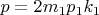
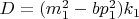 -- 02.09.2025, 11:38 --
-- 02.09.2025, 11:38 --Подставляем в формулы чисел

новые значения
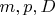
получим решение уравнения
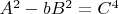
в целых числах
-- 02.09.2025, 11:53 --Если в формулах чисел
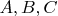
взять
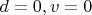
, то после всех преобразований получим:
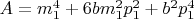
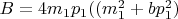
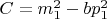
при
 -- 02.09.2025, 12:00 --
-- 02.09.2025, 12:00 --Если в формулах чисел

уравнения
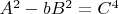
взять

,то получим формулы решения уравнения
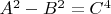
в целых числах.