Число корней уравнения 4-й степени

[nnosipov]

Сколько корней имеет уравнение $x^4-4x-6=0$ в поле $\mathbb{Z}_p$, если $p \equiv -1 \pmod{12}$?

[dmd]

0 и 2

[nnosipov]

dmd
Это верно. Есть соображения по доказательству?

[nnosipov]

Удивительно, но deepseek дико тупит на этой задаче. Даже правильный ответ дать не может. Но задача-то несложная.

[maxal]

Gemini с наводящими вопросами решает так:

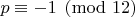
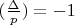
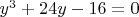
Как мы установили ранее, для простого числа $p \equiv -1 \pmod{12}$: ​Дискриминант $\Delta$ является квадратичным невычетом: $(\frac{\Delta}{p}) = -1$. ​Резольвентная кубика $y^3 + 24y - 16 = 0$ имеет ровно один корень $y_0$ в поле $\mathbb{Z}_p$. ​Сочетание этих двух фактов, согласно теории Галуа для конечных полей и теореме Штикельбергера, отсекает все варианты, кроме двух:
​Сценарий 1: 0 корней. Исходный многочлен неприводим в $\mathbb{Z}_p$. ​
Сценарий 2: 2 корня. Исходный многочлен раскладывается на два линейных множителя (дающих два корня) и один неприводимый квадратичный множитель. ​
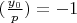
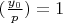
Решающее условие: корень резольвенты ​Ключевой момент, который определяет, какой из двух сценариев реализуется, — это свойство единственного корня резольвентной кубики, $y_0$. ​Если $y_0$ является квадратичным невычетом по модулю $p$ (то есть, $(\frac{y_0}{p}) = -1$), то реализуется сценарий с 0 корнями. ​Если $y_0$ является квадратичным вычетом по модулю p (то есть, $(\frac{y_0}{p}) = 1$), то реализуется сценарий с 2 корнями.

[nnosipov]

Да, все верно, Gemini молодец, если сам вспомнил про теорему Штикельбергера (deepseek ее не упоминал, поэтому его рассуждения нельзя было считать доказательством). Хотя в данном случае можно просто явно выписать корни по методу Феррари и проанализировать их. Утверждение о числе корней верно для любого нечетного простого $p \equiv -1 \pmod{3}$, но в случае $p \equiv -1 \pmod{12}$ мы можем по простым формулам находить квадратные и кубические корни в поле $\mathbb{Z}_p$ (иными словами, можем решить уравнение $x^4-4x-6=0$ прямо по формуле для корней).