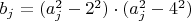Функция Эйлера хорошо изучена, поэтому не буду на ней задерживаться.
Единственное приведу ее развернутый вид, приведенный к примориалам, и который не встречал:
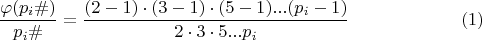
Умножив (1) на

и развернув его, получаем:
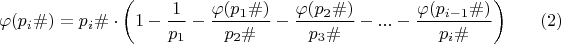
Для расчета количества
пар чисел-близнецов, взаимно простых с примориалом, я ранее в одной из своих тем предложил использовать
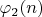
:
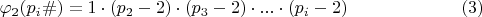
Ее развернутый вид для примориалов:
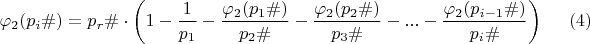
При этом надо отметить, что (3) дает завышение

для каждого из примориалов.
Чтобы найти конкретные значения таких взаимно простых пар, необходимо прогнать числа
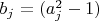
по моулям соотвтствующих примориалу простых (где

- натуральные числа,

- порядковый номер в ряду натуральных чисел от

до

). В итоге такого расчета будут получаться произведения чисел-близнецов.
По формуле (3) также можно подсчитать количество взаимно простых к примориалам
чисел-кузенов (отличающихся на

)
В этом случае (3) дает точное значение.
Поэтому в примориалах число взаимно простых кузенов на 1 больше числа взаимно простых близнецов.
Чтобы найти конкретные значения таких взаимно простых пар, необходимо прогнать числа
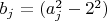
.
Чтобы подсчитать количество чисел взаимно простых примориалу, но
отличающихся друг от друга на 
, используем формулу немного отличающуюся от (3):
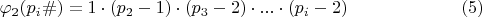
Погрешность (5)

.
Здесь
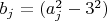
Как видно из сравнения (3) и (5) таких чисел практически в два раза больше, чем чисел-близнецов.
Приведу еще функцию
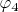
для расчета взаимно простых примориалу
для квадруплетов:
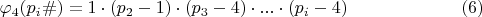
Здесь