Броски до двух единиц

[artempalkin]

Я бросаю монету до тех пор, пока не выпадет два орла подряд (пусть будет две единицы). Сколько в среднем бросков потребуется?
Я поднимал уже такие темы на форуме, но сейчас вопрос не в решении этой конкретной задаче, а в обосновании метода решения.

Вообще задача решается не так уж очевидно. То есть эту СВ на сумму СВ как-то не особо разложишь. Считать вероятности для каждого возможного количества бросков, закончившимся двумя единицами, - удовольствие небольшое (для двух единиц это не так сложно, но если их больше... становится реально тяжело). Но тут приходит на помощь невероятный метод, подсказанный уважаемым участником Shadow.

Пусть $m$ - искомое среднее значение. Тогда:

$m = \frac12(1+m)+\frac12\left(\frac12(2+m)+\frac122\right)$

Эта великая в своей простоте формула выражает дерево вариантов. Из нее найти $m$ - вопрос пары секунд. Естественно, для более сложных случаев все будет сложнее, но все равно это намного проще, чем любые другие методы, какие я могу себе представить.

Но откуда по существу берется эта формула? По идее она должна быть следствием соотношения СВ между собой. Но СВ между собой не соотносятся через вероятности!

[TOTAL]

artempalkin в сообщении #1699789 писал(а):

Но СВ между собой не соотносятся через вероятности!

1. Я бросаю монету до тех пор, пока не выпадет два орла подряд. Сколько в среднем бросков потребуется?
2. Я бросаю монету до тех пор, пока не выпадет два орла подряд. Сколько в среднем бросков потребуется, если первой выпала решка?
Ответы на эти вопросы связаны между собой.

[artempalkin]

TOTAL
спасибо, я формулу написал как раз исходя из этой "связи" ответов. Но по существу я не понимаю, откуда эта формула следует (то есть не в плане некоторого здравого смысла, а четких математических формул). Похоже, что она следует из формулы полной вероятности (как бы очень похожа на нее), но формула полной вероятности связывает вероятности, а не СВ или их матожидания.

[TOTAL]

artempalkin в сообщении #1699802 писал(а):

связывает вероятности, а не СВ или их матожидания.

Запишите матожидание через вероятности для обех задач. Затем выразите вероятности для одной задачи через вероятности для другой задачи (ведь они связаны!). Так и увидите связь между матожиданиями.

[dsge]

artempalkin в сообщении #1699802 писал(а):

Но по существу я не понимаю, откуда эта формула следует

artempalkin в сообщении #1699789 писал(а):

$m = \frac12(1+m)+\frac12\left(\frac12(2+m)+\frac122\right)$

Берется из рассуждений и формулы полной вероятности:
1. $m$ - нужное матожидание количества бросков.
2. Вы ничего не бросаете, а оно уже есть (слева).
3. Вы сделали один бросок, выпала решка с вероятность 1/2, вы опять в начале пути и мат ожидание количества шагов, с этого шага будет опять $m$, эта решка не учитывается в дальнейшем. Но один шаг уже сделан, поэтому его надо добавить к $m$. Получаем то что стоит с права $\frac12(1+m)$.
4. Если в первый бросок выпал орел, вероятность 1/2 - множитель перед вторым слагаемым справа, то вторым броском все закончится с вероятностью 1/2, если опять будет орел - $\frac122$ второй орел - итого 2 броска умноженные на вероятность этого события.
5. Если после первого орла выпала решка, то вы опять в начале пути, с этого шага среднее число бросков опять будет $m$, но надо учесть, что 2 броска уже сделано, поэтому стоит $2+m$.

[mihaild]

Если совсем формально.
Пусть $\xi_i$ - число бросков, начиная с $i$-го, пока не выпадет два орла подряд. Нас интересует $\mathbb \xi_1$.
Пусть $t_i = 1$ если на $i$-м броске выпал орел, и $0$ если решка.
Понятно, что все $\xi_i$ одинаково распределены, все $t_i$ одинаково распределены, и что $t_i$ независимо с $\xi_j$ при $j > i$.
Верно равенствно случайных величин (вот тут дерево вариантов): $\xi_i = (1 - t_i) \cdot \xi_{i + 1} + t_i \cdot ((1 - t_{i + 1})\cdot(2 + \xi_{i + 2}) + t_{i + 1} \cdot 2)$.
Навесив на обе части мат. ожидание, получаем Вашу формулу.

[artempalkin]

dsge
Спасибо, но это я все понимаю. Я не списал эту формулу откуда-то, а записал ее сам именно из тех соображений, которые вы перечислили :)

mihaild в сообщении #1699824 писал(а):

Если совсем формально.
Пусть $\xi_i$ - число бросков, начиная с $i$-го, пока не выпадет два орла подряд. Нас интересует $\mathbb \xi_1$.
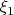
Пусть $t_i = 1$ если на $i$-м броске выпал орел, и $0$ если решка.
Понятно, что все $\xi_i$ одинаково распределены, все $t_i$ одинаково распределены, и что $t_i$ независимо с $\xi_j$ при $j > i$.
Верно равенствно случайных величин (вот тут дерево вариантов): $\xi_i = (1 - t_i) \cdot \xi_{i + 1} + t_i \cdot ((1 - t_{i + 1})\cdot(2 + \xi_{i + 2}) + t_{i + 1} \cdot 2)$.
Навесив на обе части мат. ожидание, получаем Вашу формулу.

О, спасибо, это похоже на правду.
Меня смущает одна вещи: $\xi_i$ - это все же не вполне то, что вы записали.

mihaild в сообщении #1699824 писал(а):

Пусть $\xi_i$ - число бросков, начиная с $i$-го, пока не выпадет два орла подряд.

Строгое определение $\xi_i$ не может быть таким, т.к. к этому моменту игра может уже закончиться, к тому же предыдущим значением обязательно должен быть $0$. Вы скажете, что для этого у вас в запасе множитель $t_i$, но формально я вижу в этом изъян (если все, что угодно, умножить на $0$, то получится, конечно, $0$, но все же это должно быть что-то определенное и осязаемое).

Тогда $\xi_i$ можно определить так:
1) Она равно нулю, если игра закончилась до $i$-того хода включительно;
2) Она равна нулю, если игра не закончилась, но $i$-й бросок - единица;
3) Если первые два не выполняются, то она - "число бросков, начиная с $i$-го, пока не выпадет два орла подряд".

Если так сформулировать, то, кажется, стало яснее, спасибо!

-- 27.08.2025, 13:40 --

С другой стороны, будут ли тогда все $\xi_i$ одинаково распределены?

[mihaild]

artempalkin в сообщении #1699847 писал(а):

Строгое определение $\xi_i$ не может быть таким, т.к. к этому моменту игра может уже закончиться

Тут удобнее рассматривать немного другую игру: даже после выпадения двух орлов продолжить кидать монету (или, чтобы зря времени не терять, сразу кинуть монету бесконечное число раз, а уже потом искать в этой последовательности пару орлов). Время до двух орлов в этих двух играх одинаковое, потому что каждому исходу оригинальной игры соответствует множество исходов новой с тем же результатом и той же мерой.

[Null]

Все эти решения предполагают что матожидание конечно.

[Baltimor]

Здравствуйте, рассматривая возможные исходы при n бросках монеты и выделяя из них благоприятные, обнаружил следующую последовательность для количества благоприятных исходов Q(n): 0,1,1,2,3,5,8,.....
Неужели количество благоприятных исходов описывается числами Фибоначчи?

[Shadow]

Baltimor в сообщении #1699871 писал(а):

Здравствуйте, рассматривая возможные исходы при n бросках монеты и выделяя из них благоприятные, обнаружил следующую последовательность для количества благоприятных исходов Q(n): 0,1,1,2,3,5,8,.....
Неужели количество благоприятных исходов описывается числами Фибоначчи?

Если правильно понял вашу мысль, то вы считаете сколко $k$ -значных чисел в двоичной системе не содержат двух последовательных единиц? (к ним приписывается справо $011$ и получается, что две единицы впервые выпали на $k+3$ броске. То же самое , оканчивающие нулем с приписыванием $11$). Если так, то да - Фибоначчи.

$a_n$ - число $n$-значных чисел без $2$ посл. единицы, оканчивающие нулем, $b_n$ - оканчивывающие единицей.

$a_{n+1}=a_n+b_n$ (ноль можно приписать к любому числу)
$b_{n+1}=a_n$ (единицу можно приписать, только если число не оканчивается единицей)

Получается $a_{n+1}=a_n+a_{n-1}$

Фибоначчи.